Icosahedron Fractal


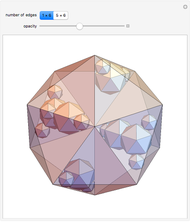
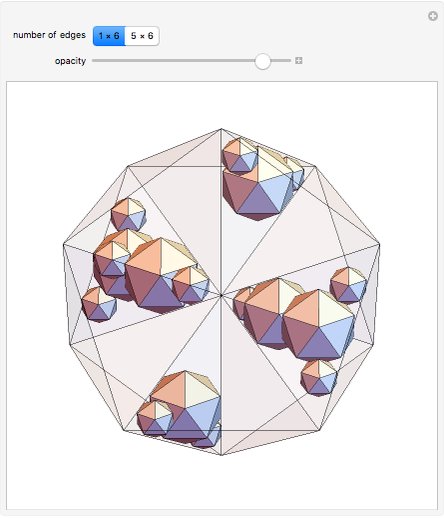
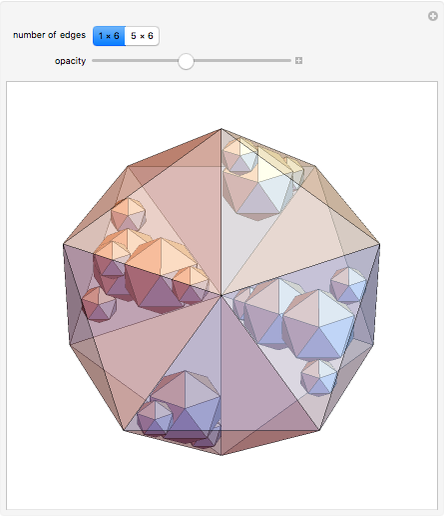
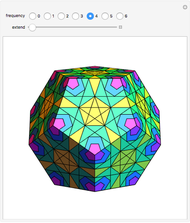
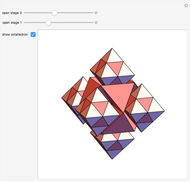
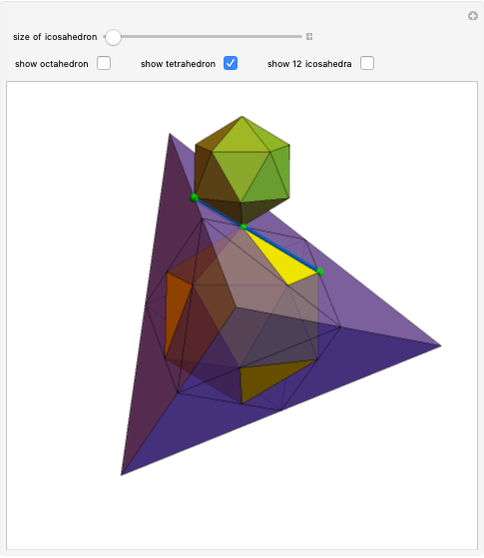
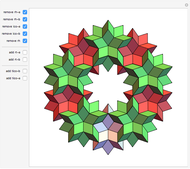
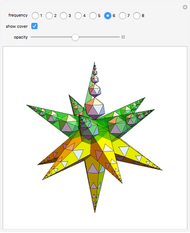
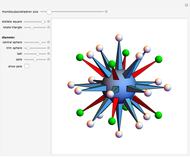
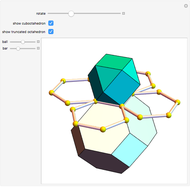
	A double tower of icosahedra is aligned along each edge of a larger enveloping icosahedron. A tower stacks gradually diminishing icosahedra on the face of an icosahedron. The rate of reduction is 1/2, and each tower could theoretically have an infinite number of icosahedra converging to a vertex of the enveloping icosahedron. Each icosahedron in the assembly could be replaced with a fractal icosahedron to form an infinite fractal structure.


	Contributed by: Sándor Kabai
	Show Initialization Code

This Demonstration can serve as a reminder of certain geometrical features—for instance, that the icosahedron has 5

6 edges, corresponding to the number of faces of the rhombic triacontahedron, and that the arrangement of 1

6 edges corresponds to the faces of the cube. The assembly is a good illustration of the self-similarity property of fractals. It also shows a geometrical example of how an infinite set of volumes can have a finite boundary. Related schoolroom exercises could include the calculation of the height of a tower, the volume of a tower, and the proportions of icosahedra.

Icosahedron (Wolfram MathWorld)

Fractal (Wolfram MathWorld)

Series (Wolfram MathWorld)

"Icosahedron Fractal" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/IcosahedronFractal/

Contributed by: Sándor Kabai

Free Download: Mathematica Player--Runs all Demonstrations & more

Browse all topics

Source page:

Name (optional)

Occupation (optional)

Organization (optional)

I use Mathematica:

often

occasionally

never

Country (optional)
Remember me

Note: Please do not include anything you consider confidential or proprietary. We will keep your information private. We will not give it to any third party.
Privacy Policy »