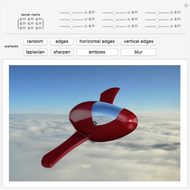
Image Kernels and Convolution (Linear Filtering)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
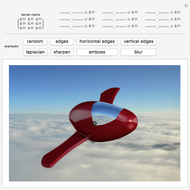
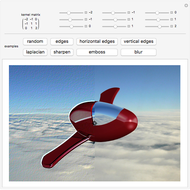
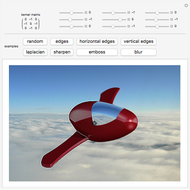
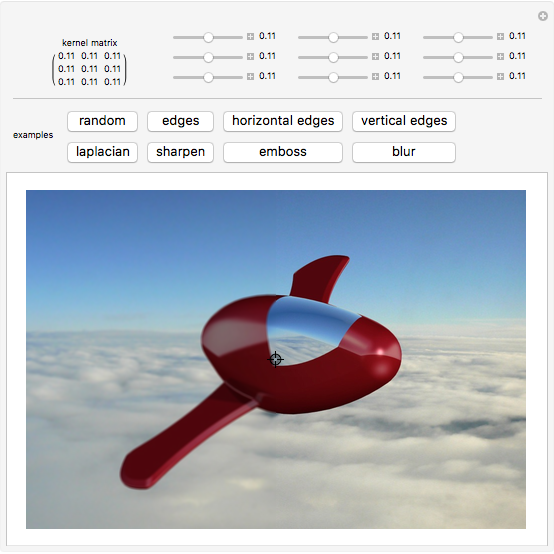
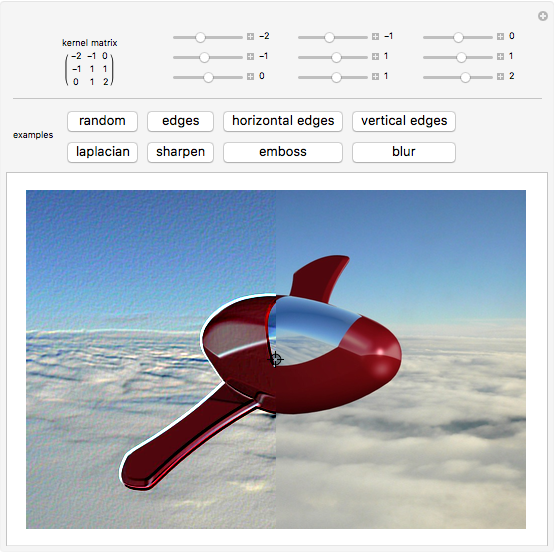
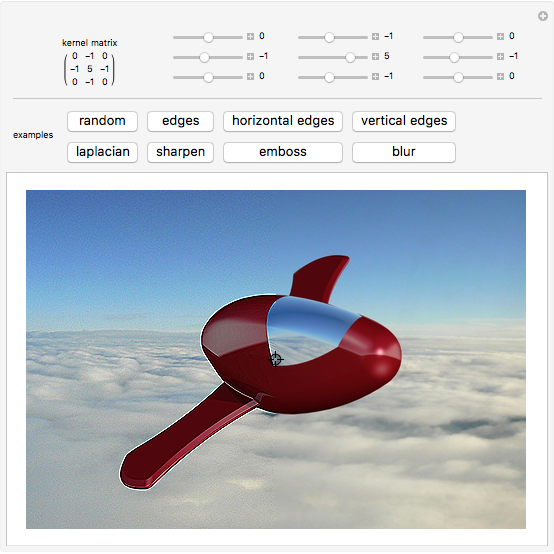
This Demonstration shows how the convolution operation can be used in conjunction with a 3×3 kernel to modify an image linearly.
[more]
Contributed by: Hector Sanchez (September 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The discrete convolution operation is defined as:
 ,
,
where  is the original image,
is the original image,  is the transformed (or filtered image),
is the transformed (or filtered image),  is the kernel to be applied to the image, and
is the kernel to be applied to the image, and  are the coordinates of the pixels.
are the coordinates of the pixels.
Suppose an image  has the grayscale pixel values
has the grayscale pixel values  and we want to transform
and we want to transform  by a kernel
by a kernel  .
.
The value of the pixel at  on the converted image
on the converted image 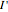 is
is  .
.
This operation of "masking" the image's pixels with the kernel values is repeated for every value of the image to obtain the transformed image 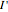 .
.
In image processing applications, masking implements linear filters; the kernels are the "recipes" from which the transformed images get their properties.
References
[1] W. Burger and M. J. Burge, Principles of Image Processing: Fundamental Techniques, New York: Springer 2009.
[2] W. Burger and M. J. Burge, Principles of Image Processing: Core Algorithms, New York: Springer, 2011.
[3] R. Szeliski, Computer Vision: Algorithms and Applications, New York: Springer, 2010.
Permanent Citation