Infinite Series Explorer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
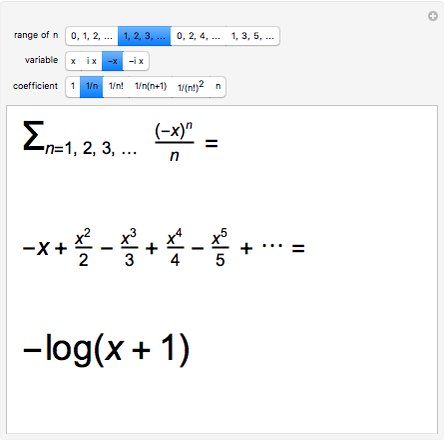
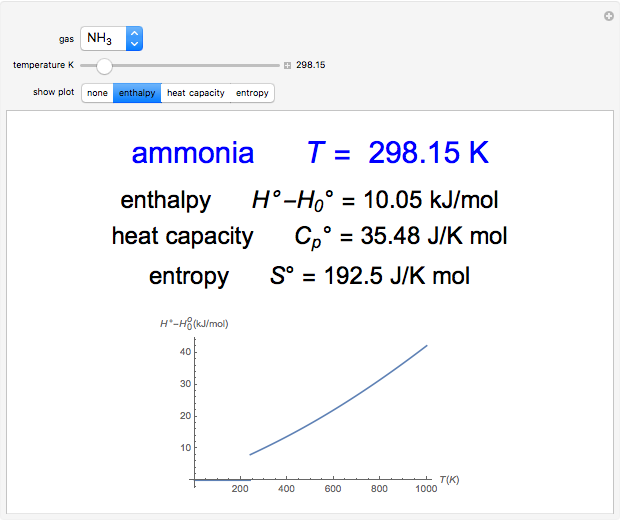
Mathematica can explicitly evaluate a large number of infinite power series. This Demonstration gives some elementary examples with simple coefficients that sum to exponential, trigonometric, hyperbolic, and logarithmic functions. Not included are hypergeometric functions, binomial expansions, inverse trigonometric functions, or Dirichlet series such as the Riemann zeta function.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
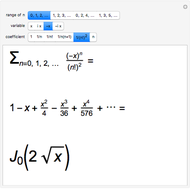
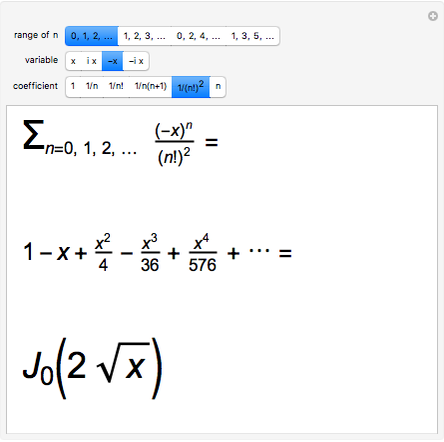
Snapshot 1: expansions of Bessel functions of zero order can be represented; higher orders would require coefficients such as 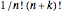
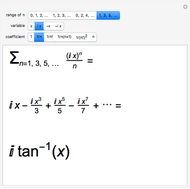
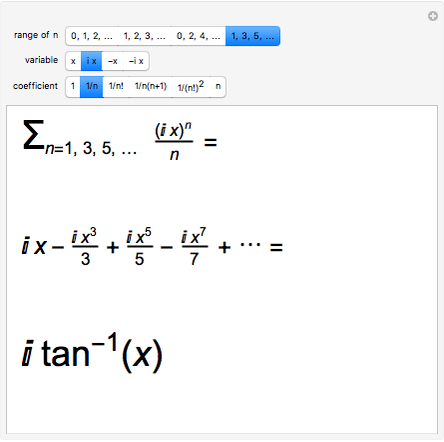
Snapshot 2: the expansion for the inverse tangent can be obtained; for 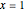 , this gives the Leibniz-Gregory series
, this gives the Leibniz-Gregory series 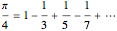
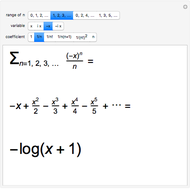
Snapshot 3: for 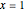 , this gives the series
, this gives the series 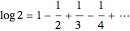
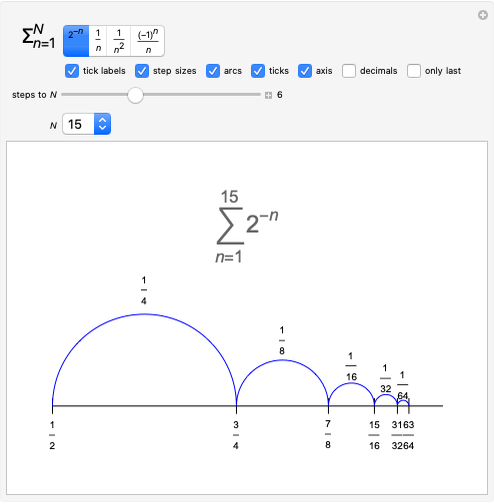
Snapshot 4: the simplest geometric series, convergent for 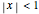
Permanent Citation