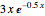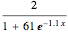Instantaneous Rate of Change: Exploring More Functions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
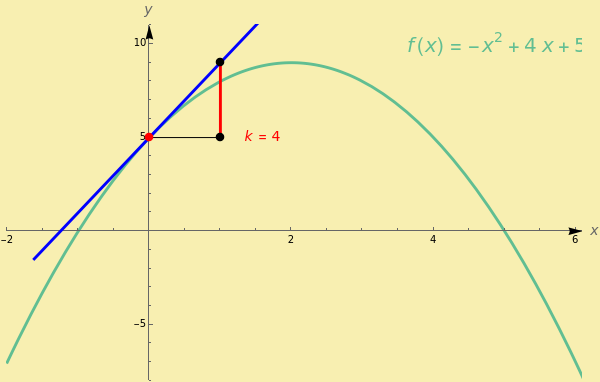
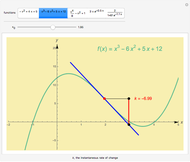
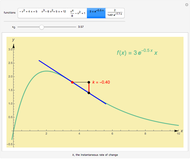
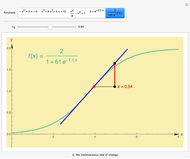
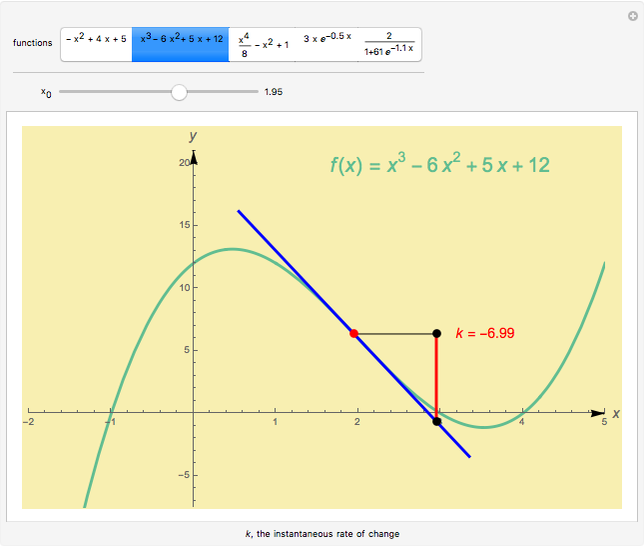
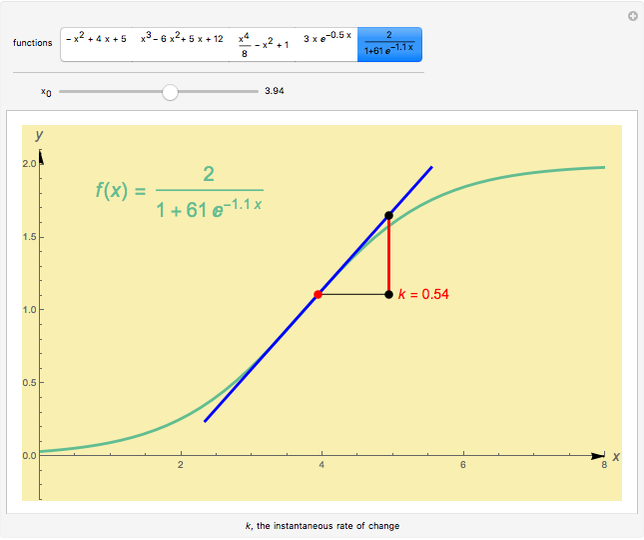
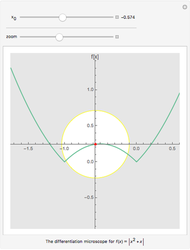
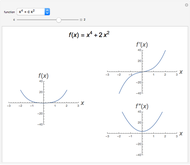
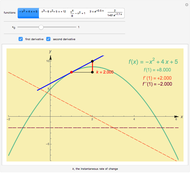
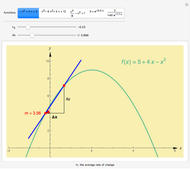
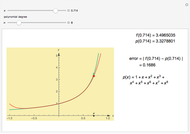
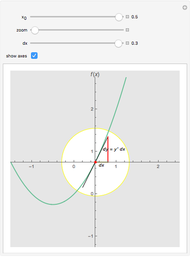
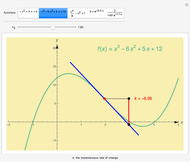
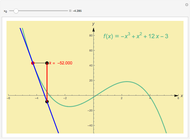
This Demonstration shows the instantaneous rate of change of  for different
for different  values for polynomial functions of degree 2, 3, and 4, an exponential function, and a logistic function.
values for polynomial functions of degree 2, 3, and 4, an exponential function, and a logistic function.
Contributed by: Wolfgang Narrath and Reinhard Simonovits (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation