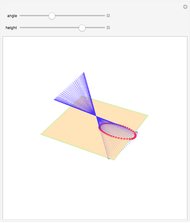
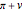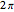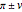Intersecting a Rotating Cone with a Plane
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
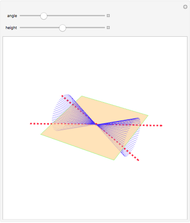
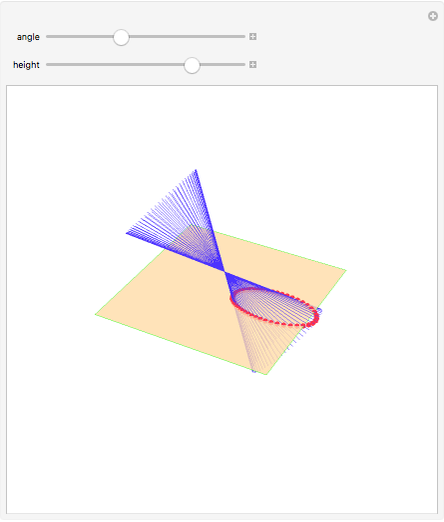
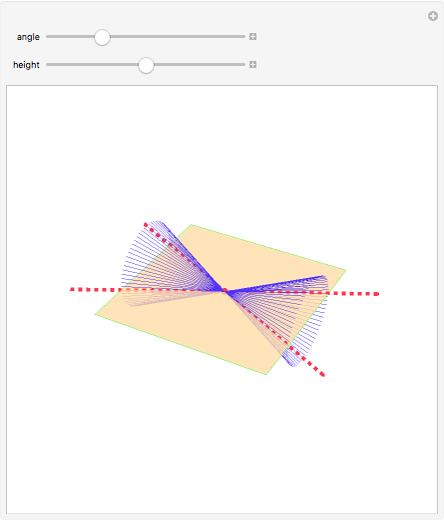
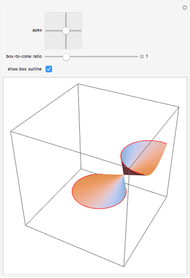
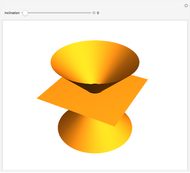
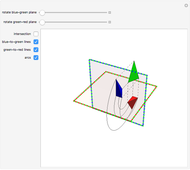
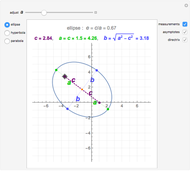
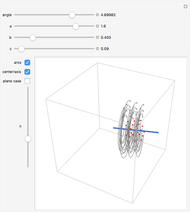
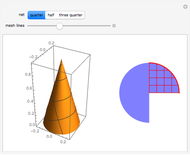
If the center of the cone is in the plane, the intersection is a point, a straight line, or a pair of straight lines, depending on the angle of the axis of the cone.
[more]
Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Intersecting a Rotating Cone with a Plane"
http://demonstrations.wolfram.com/IntersectingARotatingConeWithAPlane/
Wolfram Demonstrations Project
Published: March 7 2011