Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Irreducible Gaussian Fractions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

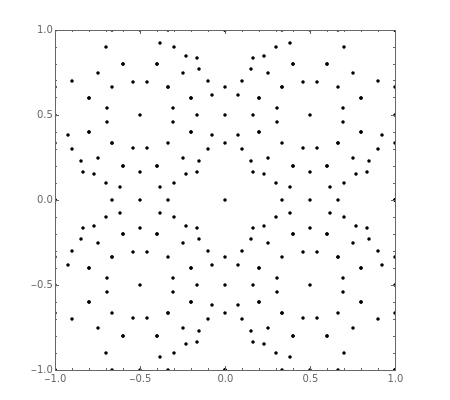
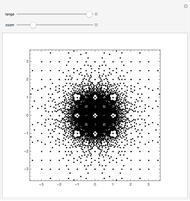
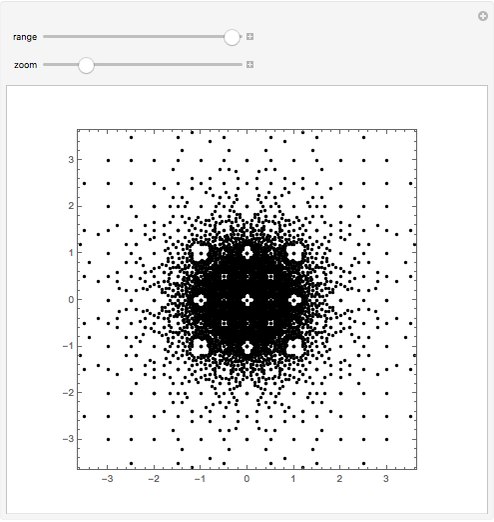
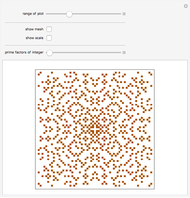
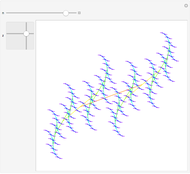
Move the sliders to see the irreducible fractions for Gaussian integers in the given range and with specified zoom level in the complex plane.

Contributed by: Eric W. Weisstein (March 2011)
Suggested by: Michael Trott
Open content licensed under CC BY-NC-SA

Snapshots

Details

An irreducible fraction is a fraction such that and have no common factor. This definition applies to ratios of ordinary integers as well as to Gaussian integers, which are of the form , where and are integers and . By rationalizing the denominator, such complex fractions can be put in the form , where and are real fractions; are the numbers plotted.

Heavily based on code by Michael Trott in The Mathematica GuideBook for Graphics New York: Springer-Verlag, 2004.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send