Kinetics of Chemical Reaction with an Intermediate Product
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
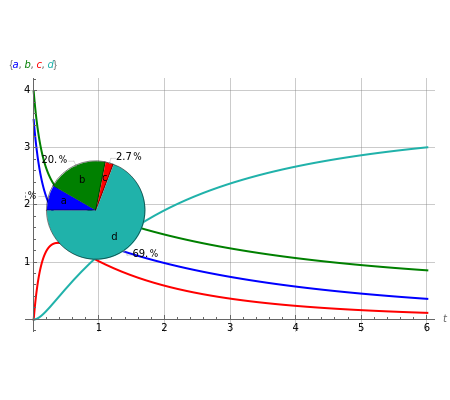
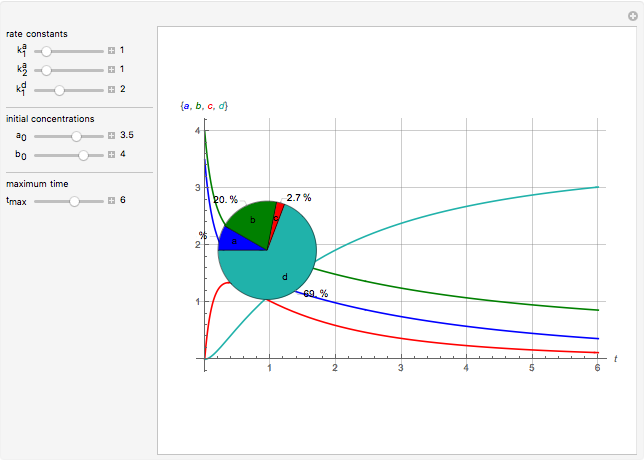
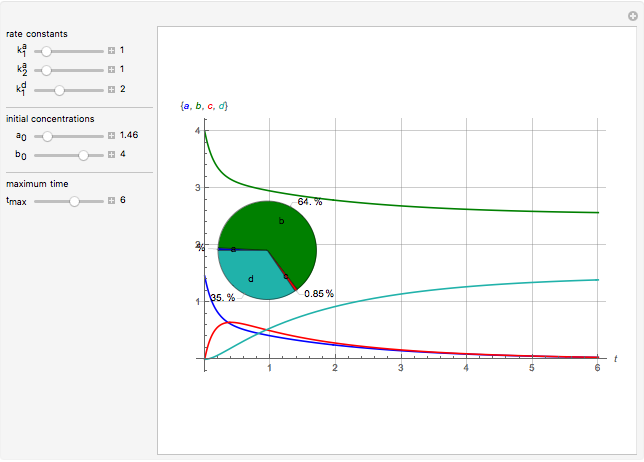
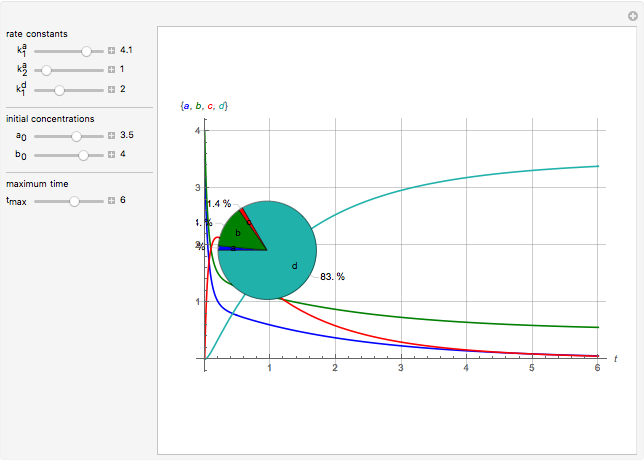
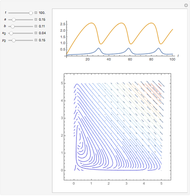
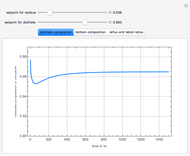
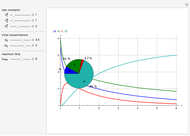
This Demonstration shows a simulation of the time course of differential rate equations. The ordinate denotes concentration in mmol/L and the abscissa denotes time in seconds. The maximum time of reactions is 
, 
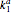and 
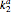are the association rate constants, 
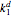is the dissociation rate constant, 
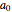and 
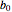are the initial concentrations of reactants 
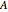and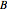 
at time 
. The pie chart shows concentrations at time in percentage terms.
Contributed by: Vladimir Gantovnik and Cynthia Gibas (University of North Carolina at Charlotte, Department of Bioinformatics & Genomics) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
After work by I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Weinheim: Wiley-VCH, 2003.
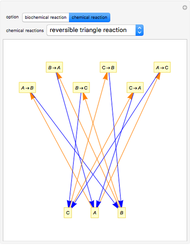
These reactions present the simplest possible reaction in heterogeneous catalysis:
,
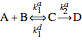where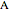 
and 
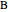are the reactants, 
is the intermediate product,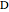 
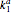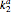is the final product, and are the association rate constants, and 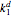is the dissociation rate constant. The system of differential equations has the following form:
,
,
,
,
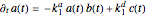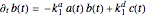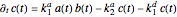where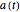 
, 
, 
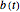, and 
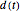are the concentrations of , , 
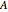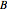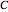, and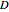 
, respectively. Initial conditions at time are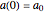 
, 
, 
, 
.
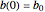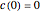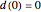Permanent Citation
Maximizing Conversion to an Intermediate Product in a Chain of Three CSTRs in Series
Clay Gruesbeck
Michaelis-Menten Enzyme Kinetics and the Steady-State Approximation
Brian M. Frezza
Why Density Change Cannot Be Ignored in a Plug Flow Reactor (PFR)
Rachael L. Baumann
The Schnakenberg Reaction
Enrique Zeleny
Driving a Reaction by Chemical Coupling
Housam Binous, Mohammad Mozahar Hossain, and Ahmed Bellagi
Volpert Graph of Chemical Reactions
Attila Nagy
Arrhenius Equations for Reaction Rate and Viscosity
Mark D. Normand, Maria G. Corradini, and Micha Peleg
Idealized Belousov-Zhabotinsky Reaction
Luca Zammataro
Reaction Factor for Second-Order Gas-Liquid Reactions
Housam Binous and Abdullah A. Shaikh
Dual Product Control of a Binary Distillation Column
Housam Binous, Naim Faqir, and Eid Al-Mutairi
