Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Knot Pattern Similar to a Lotus Kolam

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

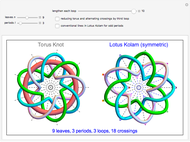
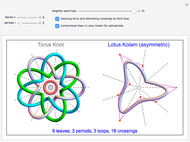
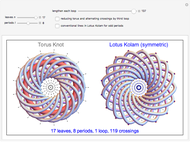
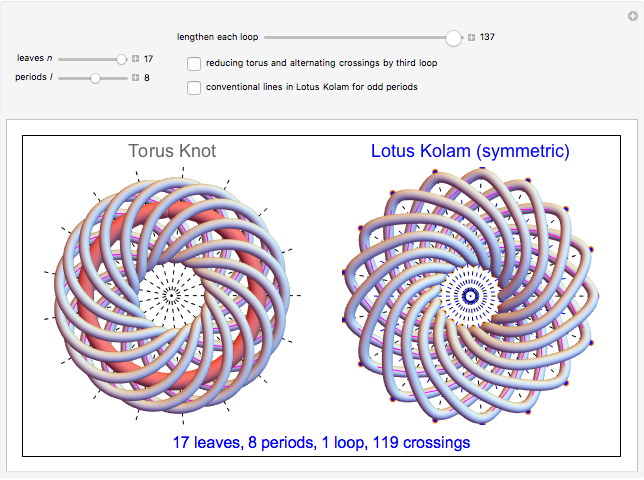
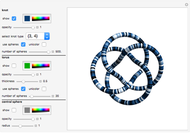
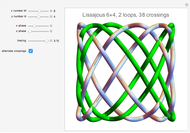
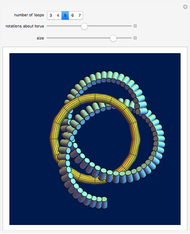
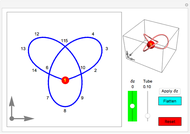
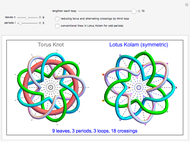
This Demonstration shows two figures. On the left is a torus knot (coil or rosette) pattern, winding a thickened curve in a spiral around a torus plotted using parametric equations.

[more]

The right graphic shows a Lotus Kolam. This variety of Kolam pattern comes mainly from Tamil Nadu, South India, and is hand drawn using a star-polygon-like framework but with different definitions (in form and process) and with more degrees of freedom. The drawings connect a dot on each adjacent radial line in sequence, and finally create a loop or multi-loop pattern.

A torus knot (without the torus) has the same topology as the Lotus Kolam. The number of components of the knot link and the loop number of the Lotus Kolam are the same as (in Mathematica given by KnotData["TorusKnot",{l,n}]), where is the number of leaves in the Lotus Kolam or turns in the torus knot, and is the number of periods in the Lotus Kolam or the torus knot.

[less]

Contributed by: Shojiro Nagata (December 2014)
InterVision Institute in Japan
Open content licensed under CC BY-NC-SA

Snapshots

Details

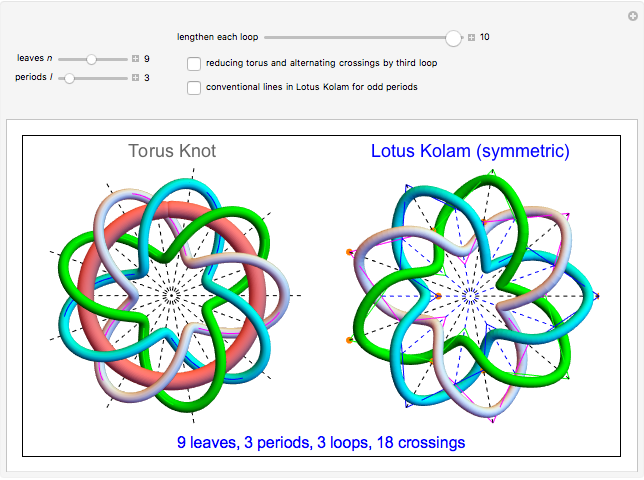
When the number of loops (components) 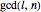is greater than 1, up to three loops are drawn, in the order: purple, green, and blue. The number of crossings is 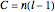. The crossings alternate if selected by the checkbox, changing the modulation frequency of 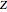to .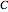

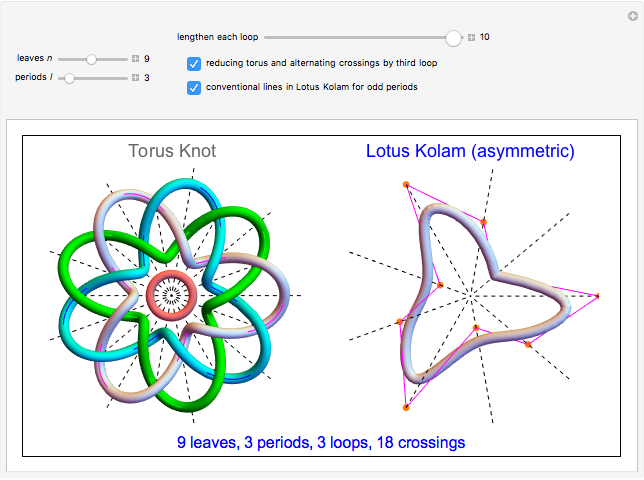
An odd period makes a symmetrical form in both the torus knot and the Lotus Kolam and has additional radial axes of half-interval angles and extra inner dots for each axis. The asymmetric form of the Lotus Kolam removes half-interval radial axes and alternating crossings and shows only one loop of odd periods.

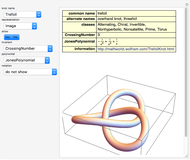
For more information on these patterns, see [1, 2]. For colored animations of some Lotus Kolams, see [3, 4].

References

[1] S. Nagata, "Loop Patterns of Lotus Kolam, Phyllotaxis, Designs in Renaissance and Knot Patterns", Forma, Special Issue 2016 (forthcoming)

[2] S. Nagata, "Loop Patterns in Japan and Asia," Forma, 30(1), 2015 pp. 19–33. www.scipress.org/journals/forma/pdf/3001/30010019.pdf.

[3] shonan0. Lotus Kolam.wmv [Video]. (Jan 21, 2016) www.youtube.com/watch?v=yao6jP8ItWc.

[4] shonan0. LotusVideo2.wmv [Video]. (Jan 21, 2016) www.youtube.com/watch?v=JZsFwUkJM5Y.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send