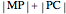Lagrange's Milkmaid Problem
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
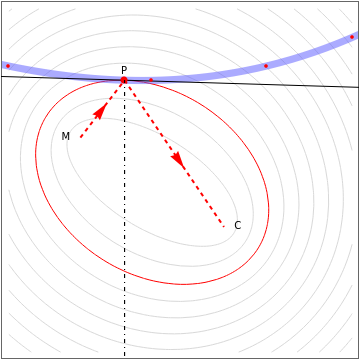
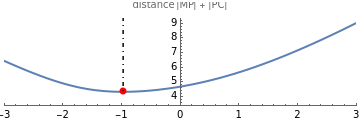
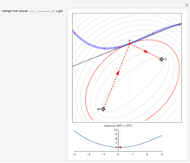
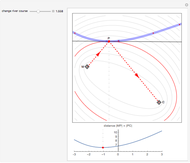
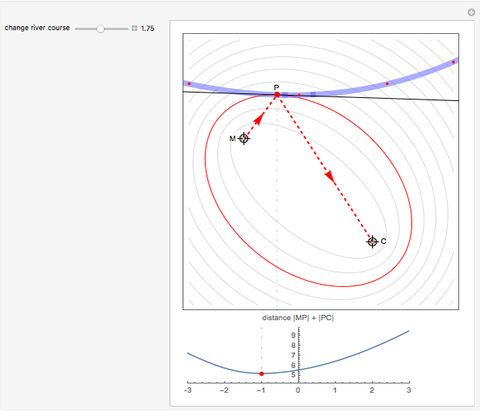
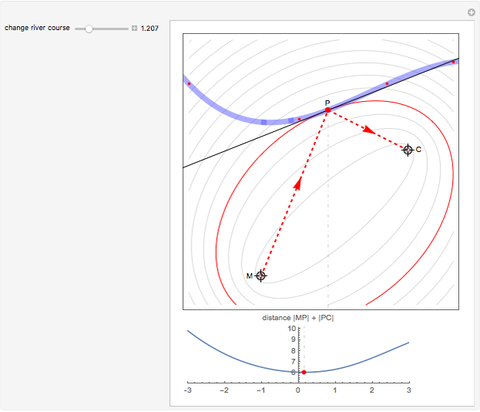
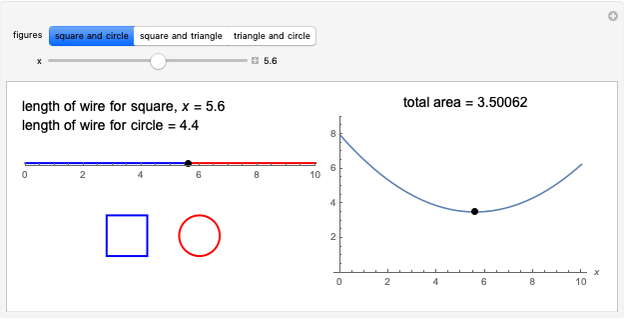
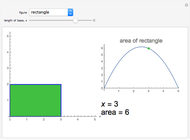
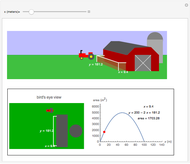
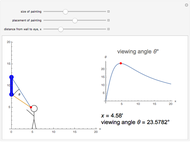
This Demonstration visualizes a classical example of constrained optimization using a Lagrange multiplier.
[more]
Contributed by: Erik Mahieu (November 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] S. Jensen. "An Introduction to Lagrange Multipliers." (2011) www.slimy.com/~steuard/teaching/tutorials/Lagrange.html.
[2] A. Segalla and S. Watson, "The Flip-Side of a Lagrange Multiplier Problem," The College Mathematics Journal, 36(3), 2005 pp. 232–235.
Permanent Citation