Laplace's Equation on a Square


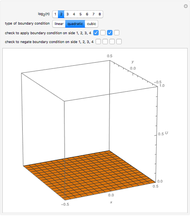
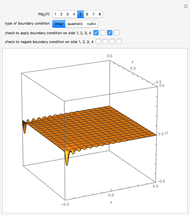
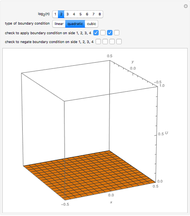
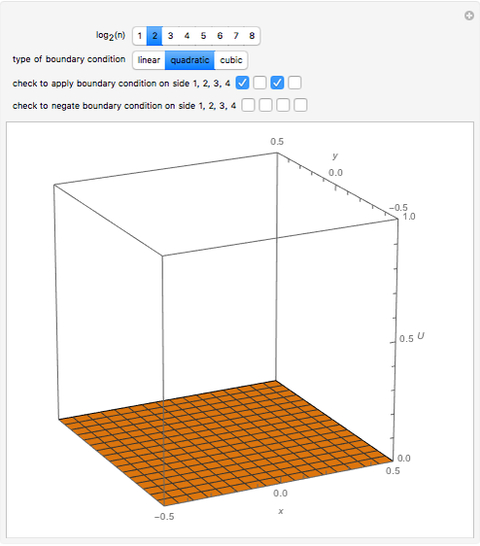
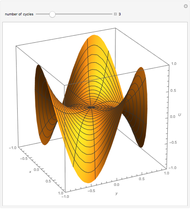
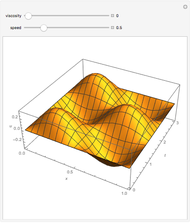
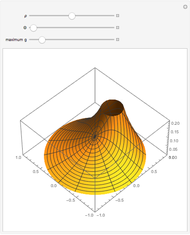
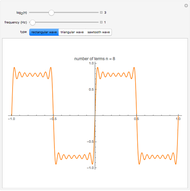
	Given Dirichlet boundary conditions on the perimeter of a square, Laplace's equation can be solved to give the surface height over the entire square as a series solution. Depending on the smoothness of the boundary conditions, vary the number of terms of the series to produce a smooth-looking surface.


	Contributed by: David von Seggern (University Nevada-Reno)

Laplace's equation in two dimensions is given by:

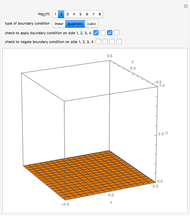
Let the unit square have a Dirichlet boundary condition

everywhere except

, where the condition is

for

. The formal solution is

where

Solutions for boundary conditions on the other sides of the square are obtained by switching variables in the formula. For instance, the solution for

applied to

for

simply switches

and

in the formula. Similar formulas are then obtained for

applied at either

, with switching

as appropriate. (Reference: E. D. Rainville, Elementary Differential Equations, 3rd ed., New York: Macmillan, 1964 p. 474)

This Demonstration deals with the square

and

by shifting the variables, leading to slightly more complicated solutions.

Solutions to Laplace's equation are called harmonic functions. One of the properties of harmonic functions is that they will not attain any local minima or maxima inside the boundary; thus the minima and maxima are on the boundary, as defined by the Dirichlet conditions. Another property is that the solution at any point