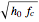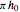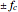Laser Lineshape and Frequency Fluctuations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
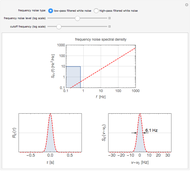
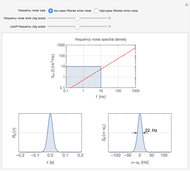
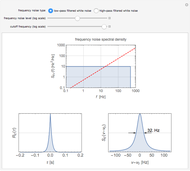
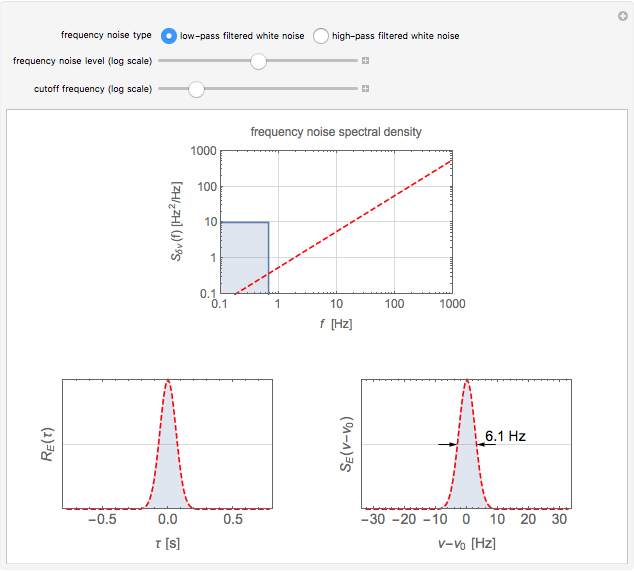
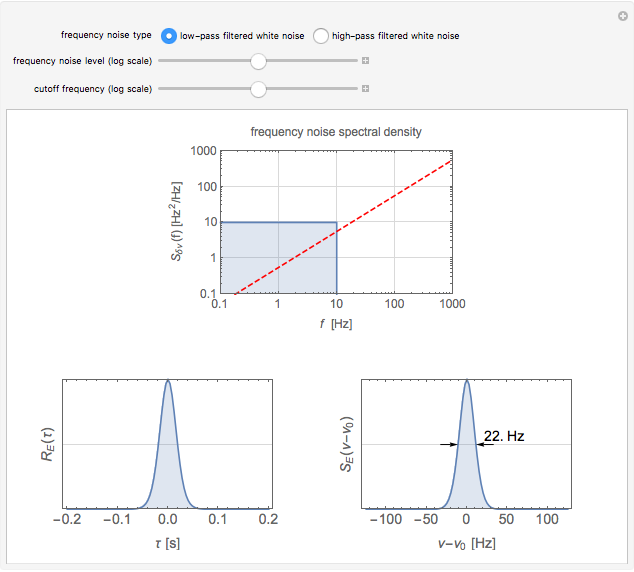
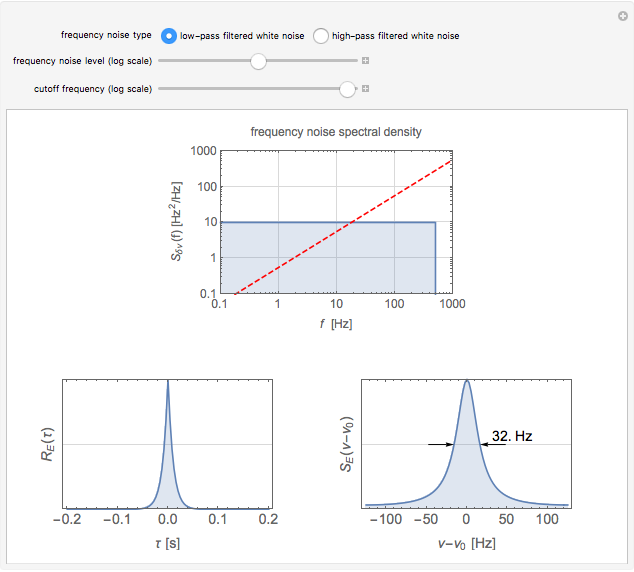
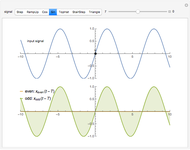
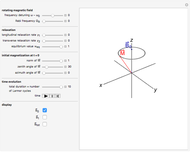
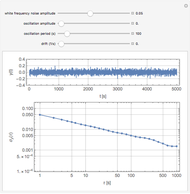
Frequency fluctuations cause the optical field of a real laser to deviate from a pure sine wave. Thus the laser is not purely monochromatic, its power spectrum showing a broadened lineshape rather than a Dirac delta function. The lineshape and linewidth depend on the spectral properties of the frequency fluctuations. This Demonstration calculates the lineshape of a laser for two distinct types of frequency noise.
[more]
Contributed by: Gianni Di Domenico (Université de Neuchâtel) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
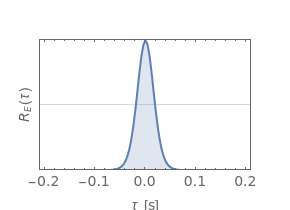
The calculation of the laser lineshape 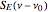 from the frequency noise spectral density
from the frequency noise spectral density 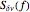 is described in D. S. Elliott, R. Roy, and S. J. Smith, "Extracavity Laser Band-Shape and Bandwidth Modification," Phys. Rev. A, 26, 1982 pp. 12–18. First, one calculates the autocorrelation function of the optical field:
is described in D. S. Elliott, R. Roy, and S. J. Smith, "Extracavity Laser Band-Shape and Bandwidth Modification," Phys. Rev. A, 26, 1982 pp. 12–18. First, one calculates the autocorrelation function of the optical field:
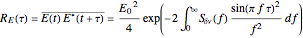 .
.
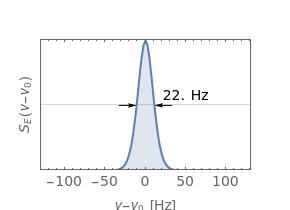
Then the lineshape is given by the Fourier transform of the autocorrelation function:
 .
.
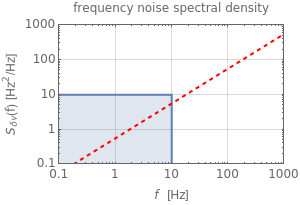
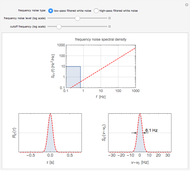
In the case of low-pass filtered white noise, that is, for a frequency noise spectral density given by
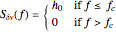 ,
,
the first integral is easy to evaluate analytically and one obtains the following expression for the autocorrelation function:
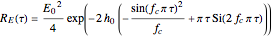 ,
,
where  is the sine integral.
is the sine integral.
In the case of high-pass filtered white noise, the frequency noise spectral density is given by
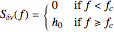 ,
,
and one obtains the following autocorrelation function:
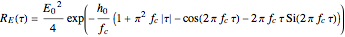 .
.
However, it is not possible to obtain an analytical expression for the Fourier transform of these autocorrelation functions. Therefore, in both cases, the laser lineshape 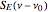 is evaluated numerically using the discrete Fourier transform.
is evaluated numerically using the discrete Fourier transform.
The red line, separating the frequency noise spectrum into two regions in which the effect of noise on the lineshape is radically different, can be determined by studying the asymptotic behavior of the two limiting cases 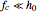 and
and  . It is given by the following equation:
. It is given by the following equation:
 .
.
Permanent Citation