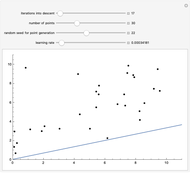
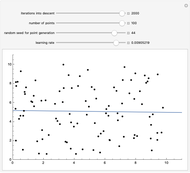
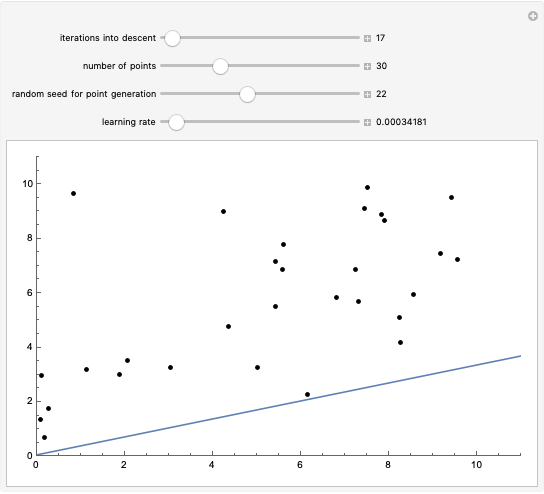
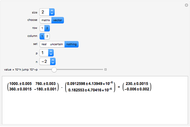
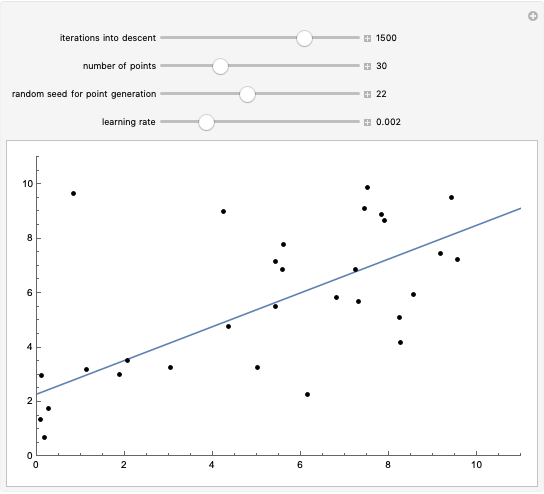
This Demonstration shows how linear regression can determine the best fit to a collection of points by iteratively applying gradient descent. Linear regression works by minimizing the error function: , where is the number of points. Because it is not always possible to solve for the minimum of this function, gradient descent is used. Gradient descent consists of iteratively subtracting from a starting value the slope at point times a constant called the learning rate. You can vary the iterations into gradient descent, the number of points in the dataset, the seed for randomly generating the points and the learning rate.