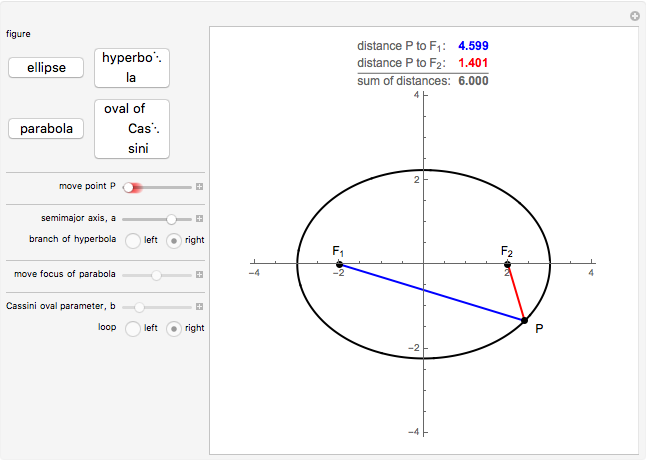
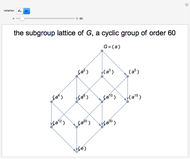
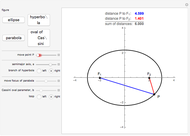
Locus of Points Definition of an Ellipse, Hyperbola, Parabola, and Oval of Cassini

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
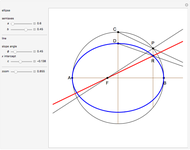
Given two points, 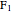 and
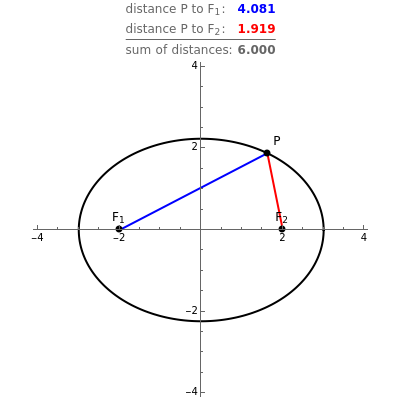
and 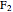 (the foci), an ellipse is the locus of points
(the foci), an ellipse is the locus of points 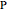 such that the sum of the distances from
such that the sum of the distances from 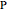 to
to 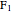 and to
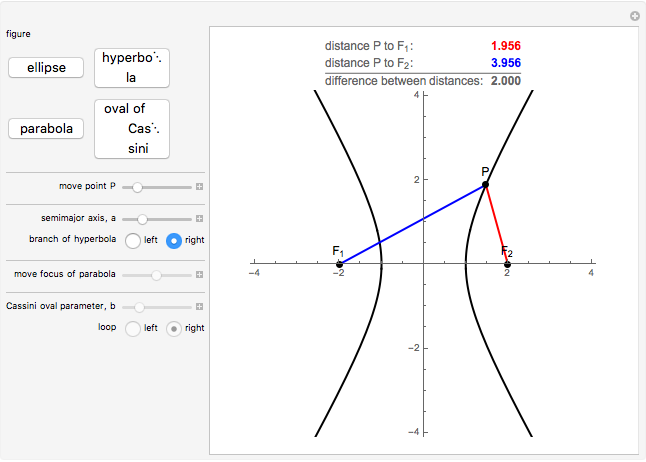
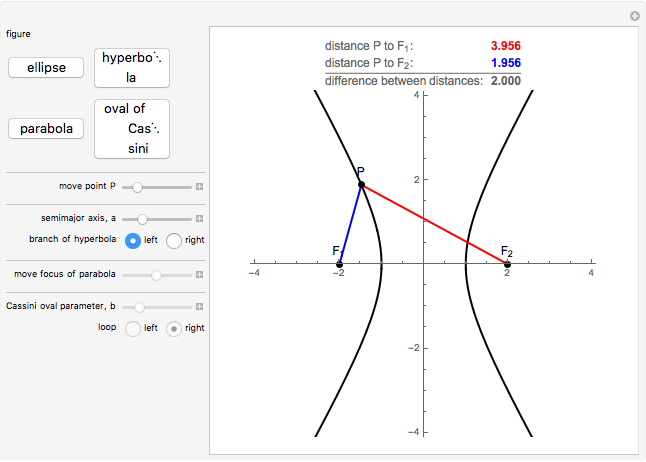
and to 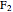 is a constant. A hyperbola is the locus of points
is a constant. A hyperbola is the locus of points 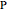 such that the absolute value of the difference between the distances from
such that the absolute value of the difference between the distances from 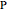 to
to 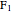 and to
and to 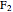 is a constant. An oval of Cassini is the locus of points
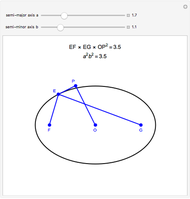
is a constant. An oval of Cassini is the locus of points 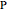 such that the product of the distances from
such that the product of the distances from 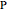 to
to 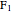 and to
and to 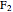 is a constant (
is a constant (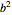 here). A parabola is the locus of points
here). A parabola is the locus of points 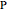 such that the distance from
such that the distance from 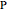 to a point
to a point 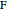 (the focus) is equal to the distance from
(the focus) is equal to the distance from 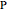 to a line
to a line 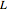 (the directrix). This Demonstration illustrates those definitions by letting you move a point along the figure and watch the relevant distances change.
(the directrix). This Demonstration illustrates those definitions by letting you move a point along the figure and watch the relevant distances change.
Contributed by: Marc Brodie (January 2011)
(Wheeling Jesuit University)
Inclusion of ovals of Cassini suggested by George Beck
Open content licensed under CC BY-NC-SA
Snapshots
Details
If the sum of the distances from a point 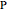 on an ellipse to the two foci is
on an ellipse to the two foci is 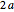 , then
, then  is the semimajor axis of the ellipse. If the absolute value of the difference between the distances from a point
is the semimajor axis of the ellipse. If the absolute value of the difference between the distances from a point 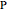 on a hyperbola to the two foci is
on a hyperbola to the two foci is 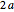 , then
, then  is the semimajor axis of the hyperbola. For ellipses and hyperbolas oriented as here, the semimajor axis of either is the distance from the origin to an
is the semimajor axis of the hyperbola. For ellipses and hyperbolas oriented as here, the semimajor axis of either is the distance from the origin to an  intercept of the figure.
intercept of the figure.
For the ovals of Cassini, if the constant  is equal to
is equal to 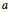 , where the distance between the two foci is
, where the distance between the two foci is 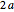 , the figure is a lemniscate. When
, the figure is a lemniscate. When 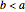 , the curve consists of two disjoint "lobes" (see snapshots 4 throrugh 6).
, the curve consists of two disjoint "lobes" (see snapshots 4 throrugh 6).
Permanent Citation