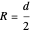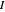Magnetic Fields for a Pair of Parallel Currents and for a Ring Current

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
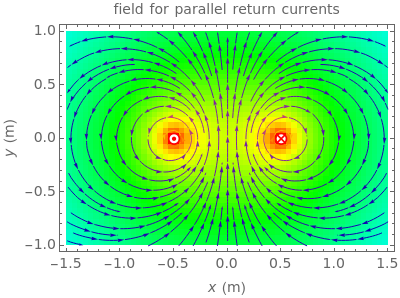
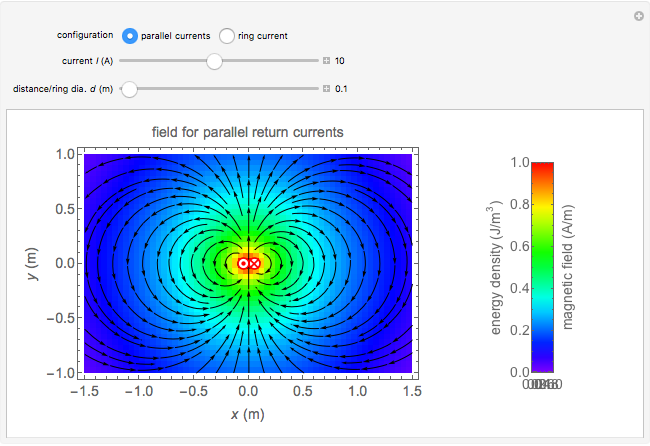
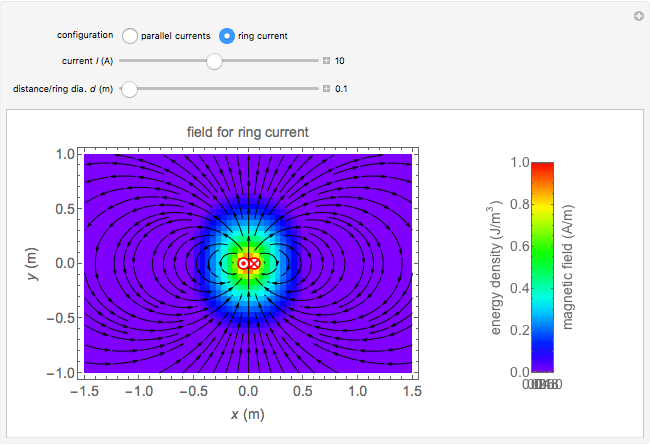
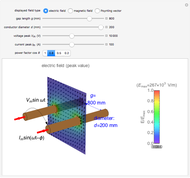
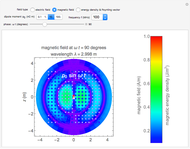
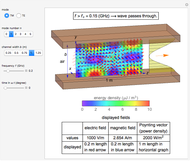
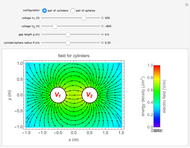
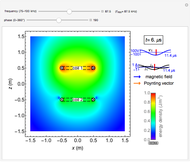
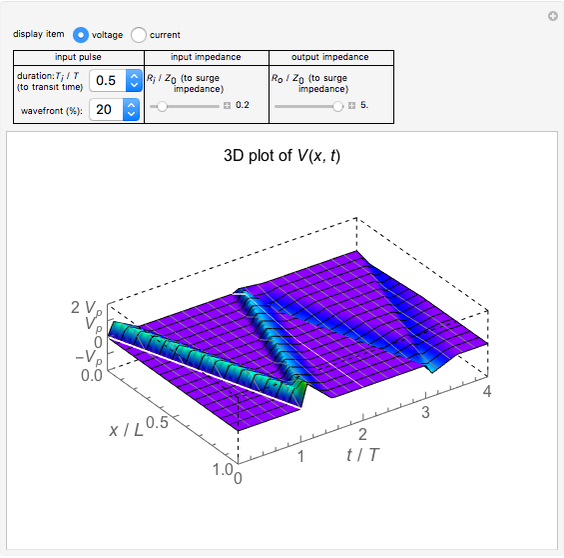
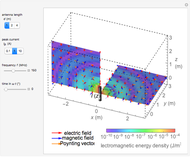
This Demonstration calculates magnetic fields for a pair of oppositely directed parallel currents and also for the cross-section of a ring current passing through the plane. The currents are assumed to be filamentary in either case.
[more]
Contributed by: Y. Shibuya (September 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
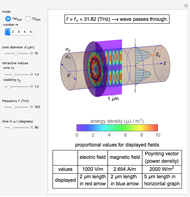
Snapshot 1: pair of opposing parallel currents  , separated by a small distance
, separated by a small distance
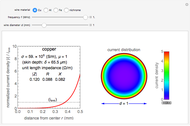
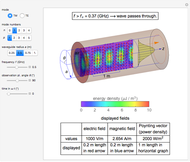
Snapshot 2: ring current of  for ring of diameter 1 m
for ring of diameter 1 m
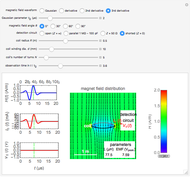
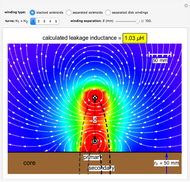
Snapshot 3: a ring current with small diameter; the field resembles that of a magnetic dipole
In the both cases, the magnetic fields are calculated from vector potential 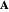 using
using 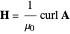 .
.
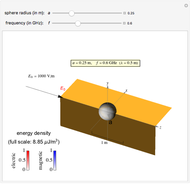
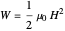 The energy density is given by
The energy density is given by 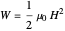 InlineMath.
InlineMath.
The vector potential 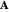 is determined as follows.
is determined as follows.
Pair of Opposing Parallel Currents
Designating the line current vector by  and the separation length by
and the separation length by 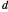 , we find
, we find 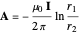 , where
, where 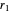 ,
, 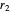 are the distances to the currents.
are the distances to the currents.
Ring Current
Using cylindrical coordinates 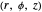 with current
with current 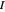 and radius
and radius 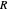 , we find
, we find 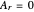 ,
, 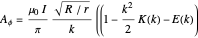 ,
, 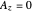 , where
, where  is the distance to the center, and
is the distance to the center, and 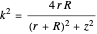 .
.
In the actual calculation, Cartesian coordinates are used and the symmetry axis is changed from  to
to 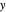 .
.
Reference
[1] G. Lehner, Electromagnetic Field Theory for Engineers and Physicists, 1st ed. (M. Horrer, trans.), New York: Springer, 2009.
Permanent Citation