Magnetic Shielding Effect of a Spherical Shell

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Consider a spherical shell of linear magnetic material with relative permeability  placed in a uniform magnetic field
placed in a uniform magnetic field  . The magnetic fields in this region can be described by a magnetic potential
. The magnetic fields in this region can be described by a magnetic potential  . Selecting the direction of
. Selecting the direction of  as the axis of spherical coordinates
as the axis of spherical coordinates 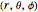 ,
,  is given by
is given by  , where
, where  is a Legendre function. The magnetic field at any point is
is a Legendre function. The magnetic field at any point is 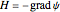 . The coefficients
. The coefficients  ,
,  in the regions with (1)
in the regions with (1)  , (2)
, (2)  , and (3)
, and (3) 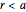 are determined by considering the boundary conditions at
are determined by considering the boundary conditions at 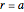 and
and 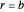 , taking into account the permeability in each region: (1) and (3)
, taking into account the permeability in each region: (1) and (3) 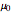 and (2)
and (2) 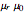 . As the result, the field in (1) is that of
. As the result, the field in (1) is that of  superimposed with the contribution of a magnetic dipole. The field in (3) turns out to be uniform, with magnitude considerably lower than
superimposed with the contribution of a magnetic dipole. The field in (3) turns out to be uniform, with magnitude considerably lower than  . The magnetic induction or B field is obtained by
. The magnetic induction or B field is obtained by 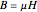 , where
, where  or
or 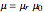 depending on the region.
depending on the region.
Contributed by: Y. Shibuya (January 2014)
Open content licensed under CC BY-NC-SA
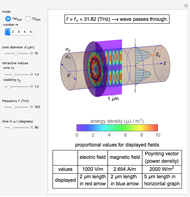
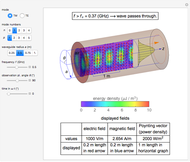
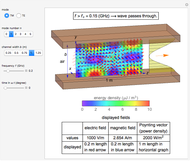
Snapshots
Details
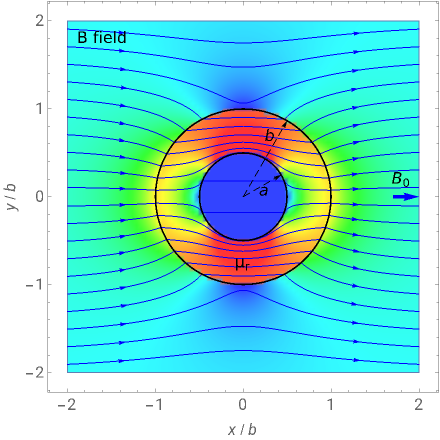
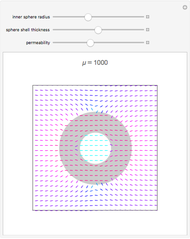
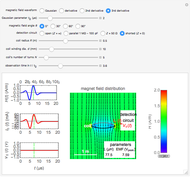
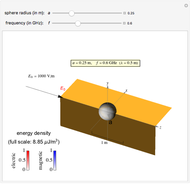
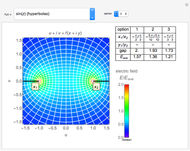
The direction of  is chosen as the
is chosen as the  axis. The fields are displayed on the cross section through the center of the spherical shell. The color represents the field intensity normalized by
axis. The fields are displayed on the cross section through the center of the spherical shell. The color represents the field intensity normalized by  . The field lines are calculated from equally distributed points. You can vary the shell's relative permeability
. The field lines are calculated from equally distributed points. You can vary the shell's relative permeability  and its configuration parameters
and its configuration parameters  ,
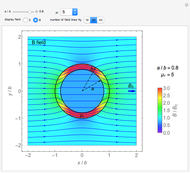
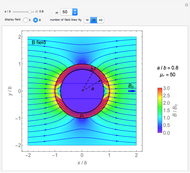
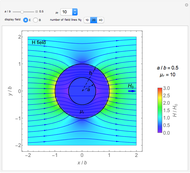
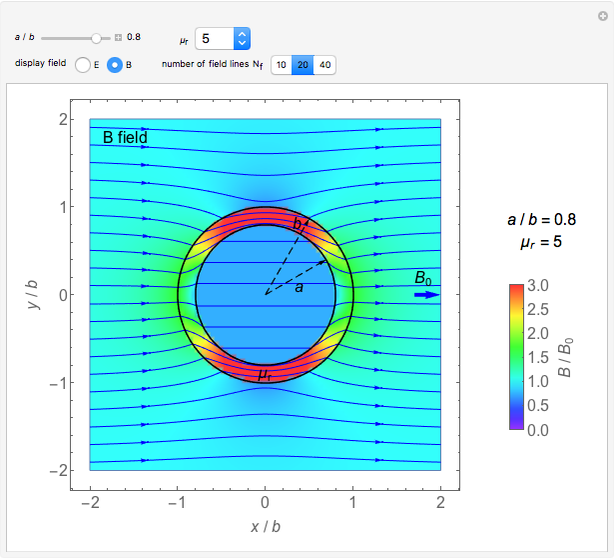
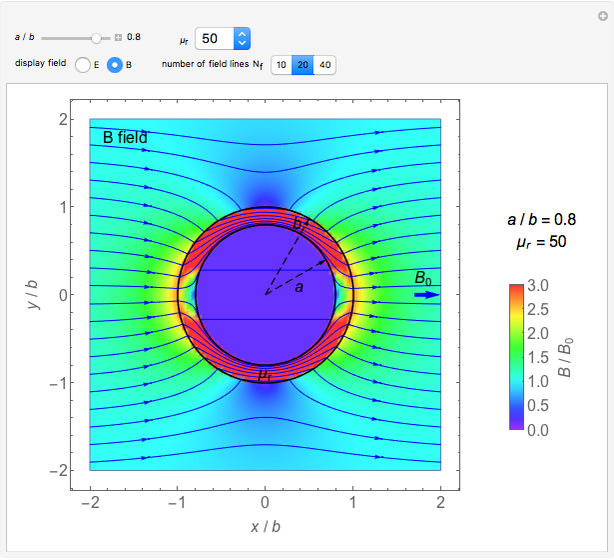
,  . It is observed that the field intensity in the inner space is greatly reduced relative to that in the outer space, especially for a large
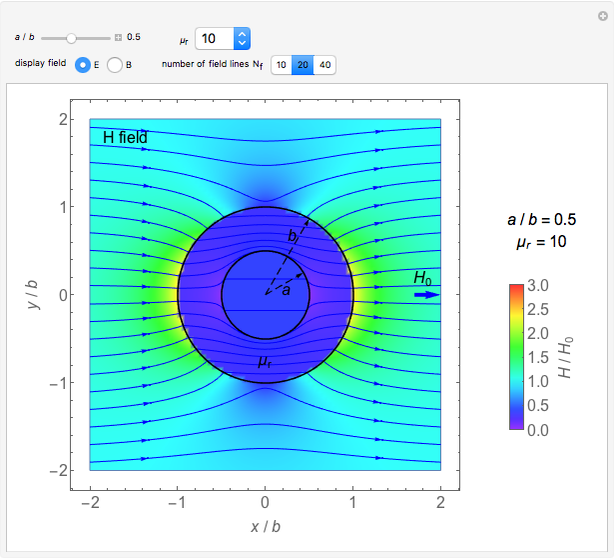
. It is observed that the field intensity in the inner space is greatly reduced relative to that in the outer space, especially for a large  . This is shown in snapshots 1 and 2. Since the E and B fields are shown in normalized bases, the two fields are equal in free space, but the E field is much smaller in the shell (magnetic medium), as shown in snapshot 3.
. This is shown in snapshots 1 and 2. Since the E and B fields are shown in normalized bases, the two fields are equal in free space, but the E field is much smaller in the shell (magnetic medium), as shown in snapshot 3.
Permanent Citation