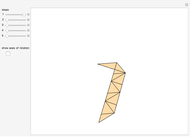
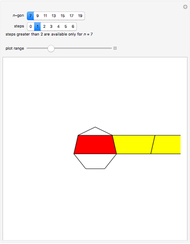
Making a Strip of Isosceles Trapezoids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
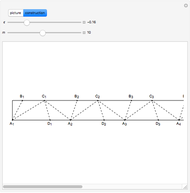
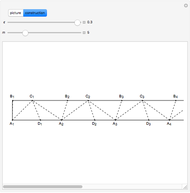
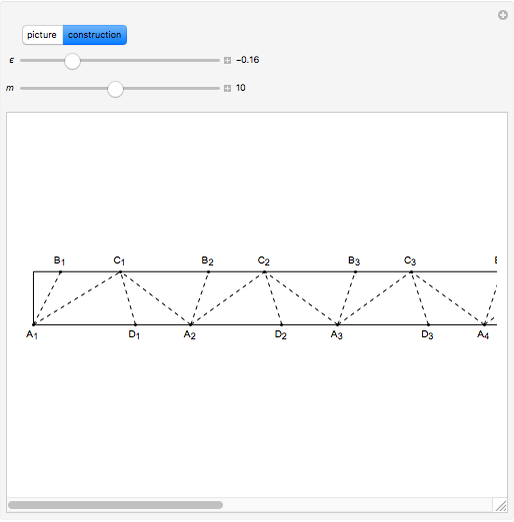
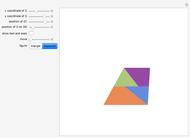
Suppose the angle  measures
measures  . The line
. The line  bisects
bisects  , so
, so  . The line
. The line  bisects
bisects  , so triangle
, so triangle  is isosceles and
is isosceles and  is congruent to
is congruent to  , which measures
, which measures  . Then
. Then  and
and  . So the angles
. So the angles  converge to
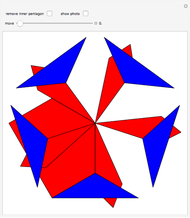
converge to  . In this way the trapezoids
. In this way the trapezoids  converge to an isosceles trapezoid congruent to the trapezoid consisting of three sides and of a diagonal of a regular pentagon. Isosceles trapezoids are obtained immediately when
converge to an isosceles trapezoid congruent to the trapezoid consisting of three sides and of a diagonal of a regular pentagon. Isosceles trapezoids are obtained immediately when  . Otherwise, the isosceles condition is approached as the number of repeats,
. Otherwise, the isosceles condition is approached as the number of repeats,  . Visually, however, the result appears to be satisfied with
. Visually, however, the result appears to be satisfied with  . Use the bottom scroll bar to view extended regions of the diagram.
. Use the bottom scroll bar to view extended regions of the diagram.
Contributed by: Izidor Hafner (January 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] P. Hilton and J. Pedersen, Build Your Own Polyhedra, Boston: Addison-Wesley, 1994, pp. 18–23.
Permanent Citation
"Making a Strip of Isosceles Trapezoids"
http://demonstrations.wolfram.com/MakingAStripOfIsoscelesTrapezoids/
Wolfram Demonstrations Project
Published: January 15 2016