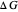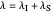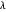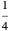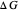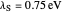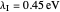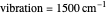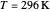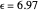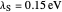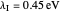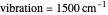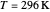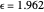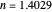Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Marcus Theory of Electron Transfer 1: Classical versus Semi-classical Models

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

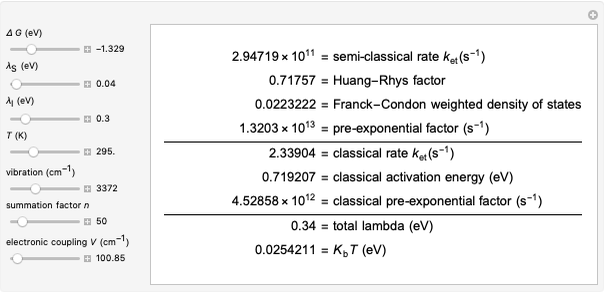
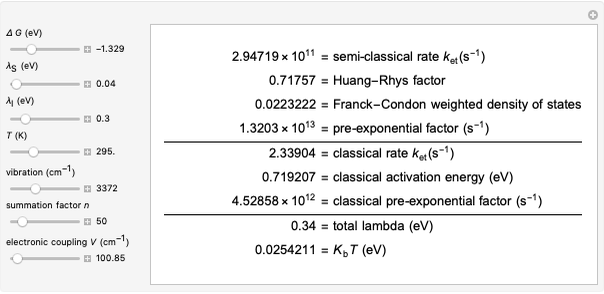
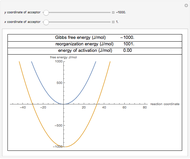
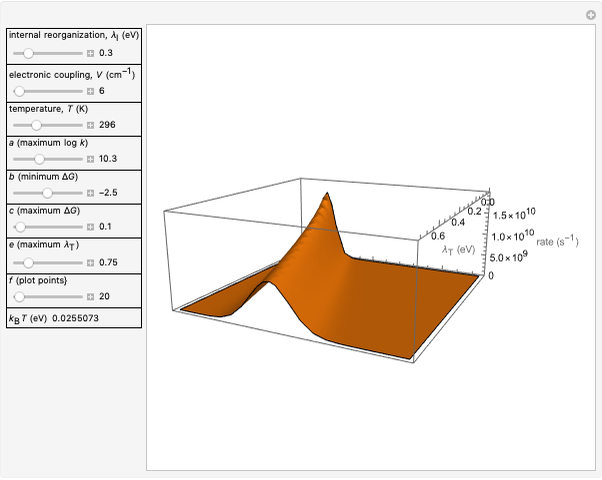
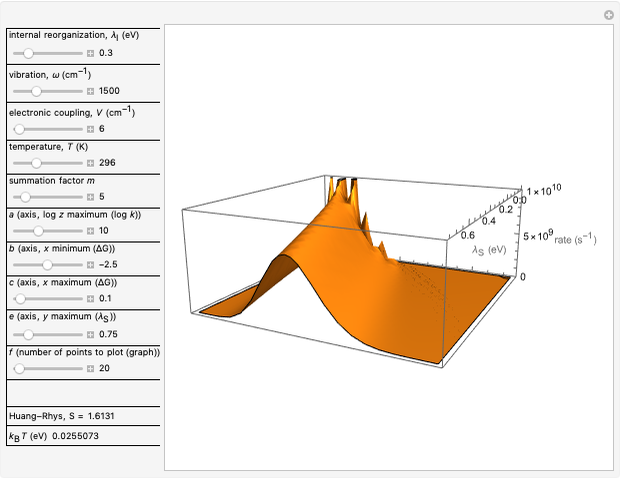
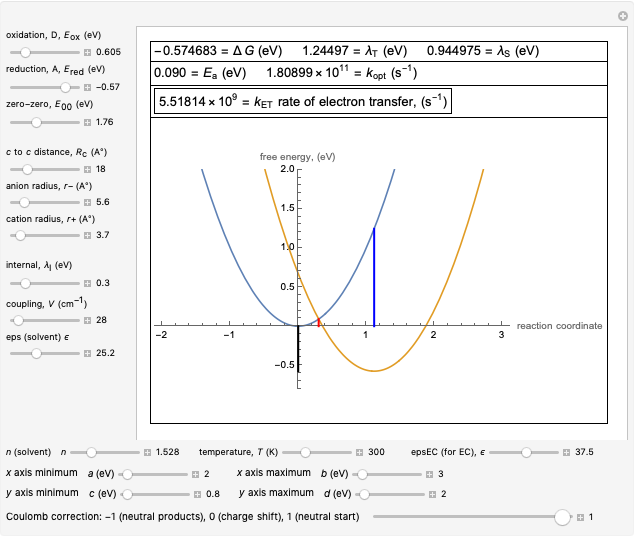
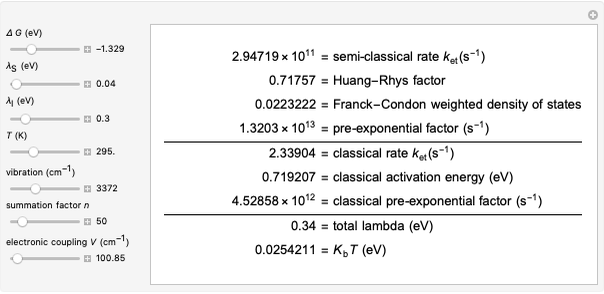
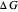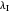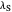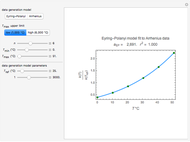
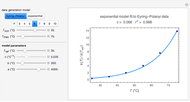
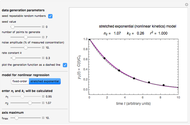
Nobel Prize winner Rudolph Marcus developed the theory of electron transfer [1]. The classical Marcus equation (CME) is based on two simultaneous quadratic relations, involving the driving force (), the internal and external (solvent) reorganization energy ( and ) and the electronic coupling (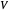). The CME underestimates the electron transfer rate in the inverted region [2, 3]. This Demonstration compares rates predicted by the classical Marcus model with those using the semi-classical Marcus model (also called Marcus–Levich–Jortner Theory, MLJ) . The starting values are from the so-called Closs and Miller data [4], which provided the first experimental proof of the inverted region. We illustrate this with the isooctane data in Snapshot 1.

[more]

We apply the semi-classical Marcus expression to the inverted region. If is much larger than the total , then inverted region effects are apparent. The enhanced rate (extra rate relative to CME) in the inverted region is related to the overlap of vibrational wavefunctions that contribute to the Franck–Condon weighted density of states (the Franck–Condon factor). The Huang–Rhys factor is related to the vibronic coupling, also called the electron-phonon coupling (often represented by the symbol S in the MLJ equation).

In Snapshot 2 (C60[3]TMPD-Tol-CR), the total is about of . The rate predicted by the CME is much too low. With the semi-classical equation, we can approach the measured rates [5] by adjusting the vibration that mediates the electron transfer (or by adjusting the electronic coupling). The other snapshots show C60[11]DMA in benzonitrile for charge separation (Snapshot 3) and charge recombination (Snapshot 4). "Initial setting" is based on Closs and Miller compounds (Snapshot 1).

Fit-values bell curve MTHF of Closs and Miller: , , , , , ,

Fit-values bell curve isooctane of Closs and Miller: , , , , , ,

The variable is in the summation factor, determining how many transfer channels contribute to the total rate [3]. The output interface also plays a role. Additional information on Marcus theory and electron transfer is available in references [6–9].

[less]

Contributed by: René M. Williams (August 2022)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Snapshot 1: Data of the first experimental proof of the inverted region (focused here on the isooctane data), based on the work of Closs and Miller.

Snapshot 2: Data on charge recombination of the compound C60[3]TMPD in toluene as solvent. The total lambda is about 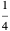of 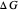. The semi-classical rate is correlated with the experimental rate. The rate predicted by the CME is much too low (~2 times per second).

Snapshot 3: Data on charge separation for the compound C60[11]DMA in benzonitrile as solvent, correlated with the experimental rate.

Snapshot 4: Data on charge recombination for the compound C60[11]DMA in benzonitrile as solvent, correlated with the experimental rate.

The output of this Demonstration was checked against the R-package [10] that runs in the statistical software package R [11] for computing and graphics.

References

[1] R. A. Marcus, "Electron Transfer Reactions in Chemistry: Theory and Experiment (Nobel Lecture)," Angewandte Chemie International Edition, 32(8), 1993 pp. 1111–1121. doi:10.1002/anie.199311113.

[2] S. Chaudhuri, S. Hedström, D. D. Méndez-Hernández, H. P. Hendrickson, K. A. Jung, J. Ho and V. S. Batista, "Electron Transfer Assisted by Vibronic Coupling from Multiple Modes," Journal of Chemical Theory and Computation, 13(12), 2017 pp. 6000–6009. doi:10.1021/acs.jctc.7b00513.

[3] P. F. Barbara, T. J. Meyer, M. A. Ratner, "Contemporary Issues in Electron Transfer Research", Journal of Physical Chemistry, 100(31), 1996 pp. 13148–13168. doi:10.1021/jp9605663.

[4] G. L. Closs and J. R. Miller, "Intramolecular Long-Distance Electron Transfer in Organic Molecules," Science, 240(4851), 1988 pp. 440–447. doi:10.1126/science.240.4851.440.

[5] P. Hudhomme and R. M. Williams, "Energy and Electron Transfer in Photo- and Electro-active Fullerene Dyads," Handbook of Carbon Nano Materials (F. D'Souza and K. M. Kadish, eds.), Hackensack, NJ: World Scientific, 2011 pp. 545–591. doi:10.1142/9789814327824_0017.

[6] R. M. Williams. "Introduction to Electron Transfer," (Nov 11, 2021) doi:10.13140/RG.2.2.16547.30244.

[7] R. M. Williams. Photoinduced Electron Transfer - The Classical Marcus Theory [Video]. (Nov 11, 2021) youtu.be/YFzeMMOvhl0.

[8] R. M. Williams. Photoinduced Electron Transfer - The Semi-classical Marcus–Levich–Jortner Theory [Video]. (Nov 11, 2021) youtu.be/GnPIbH6nM9o.

[9] R. M. Williams. University of Amsterdam. (Nov 11, 2021) www.uva.nl/en/profile/w/i/r.m.williams/r.m.williams.html.

[10] J. Idé and G. Raos. "ChargeTransport: Charge Transfer Rates and Charge Carrier Mobilities." (Nov 11, 2021) CRAN.R-project.org/package=ChargeTransport.

[11] "What Is R?" The R Foundation. (Nov 11, 2021) www.r-project.org/about.html.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send