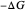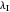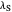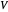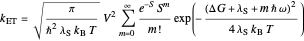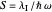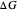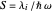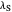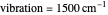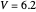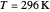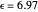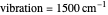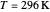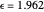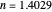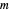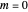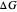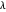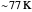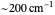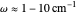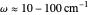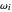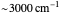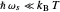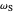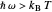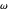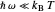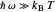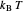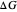Marcus Theory of Electron Transfer 2: Semiclassical Marcus Equation in Three Dimensions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
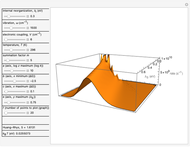
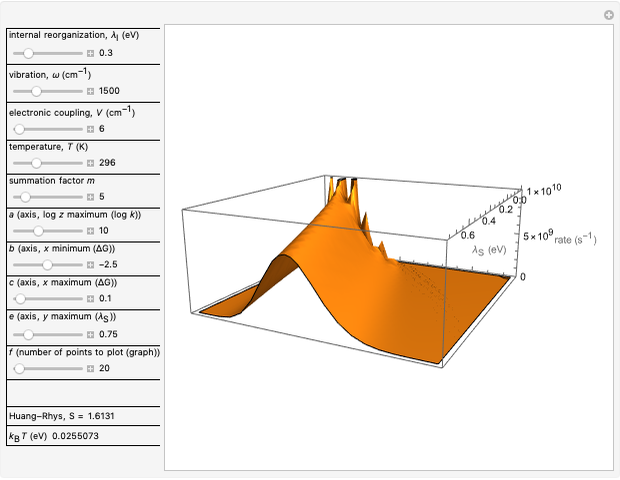
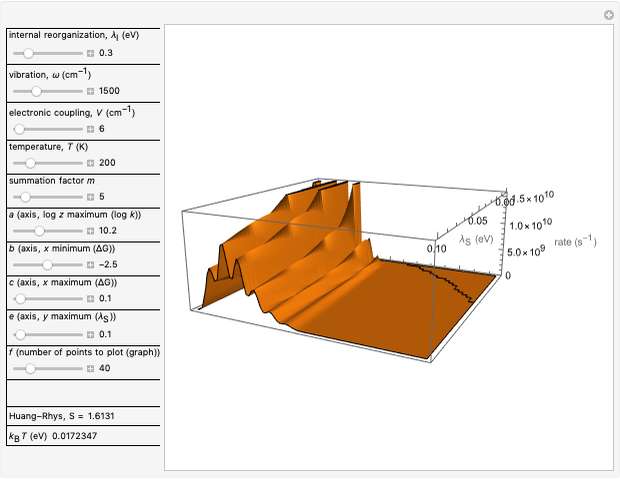
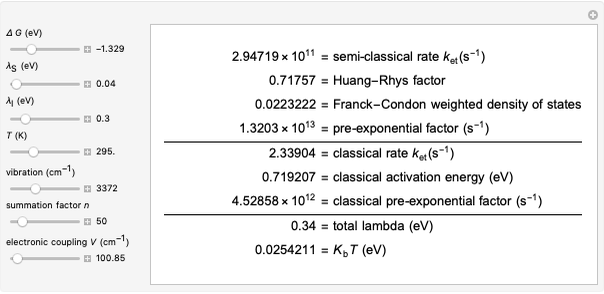
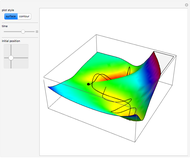
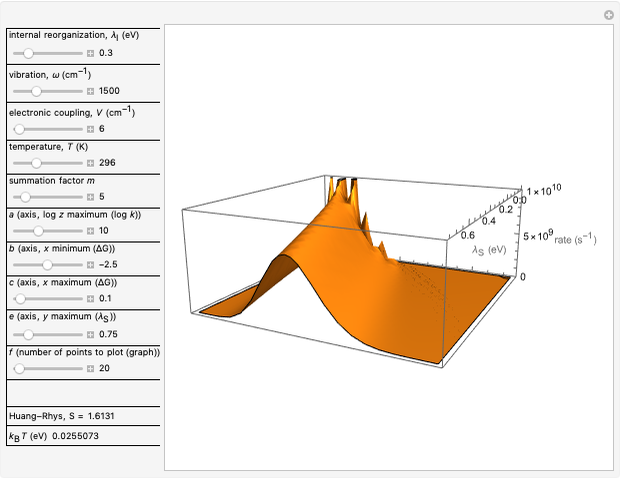
This Demonstration describes the semiclassical Marcus model (also called Marcus–Levich–Jortner Theory, MLJ) in three dimensions. The rate  on the
on the  axis is plotted as a function of the Gibbs free energy change
axis is plotted as a function of the Gibbs free energy change 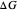 and the solvent reorganization energy
and the solvent reorganization energy 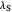 on the
on the  and
and  axes. This is a linear plot; often
axes. This is a linear plot; often 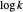 plots are used in this application.
plots are used in this application.
Contributed by: René M. Williams (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
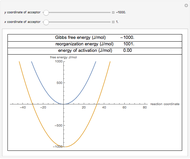
Snapshot 1: data based on the work of Closs and Miller (focused here on the isooctane data) at 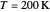 , shifting the
, shifting the  axis to 0.1 eV as the upper limit, highlighting the region with low solvent reorganization energies
axis to 0.1 eV as the upper limit, highlighting the region with low solvent reorganization energies
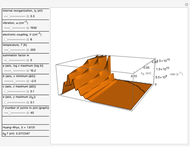
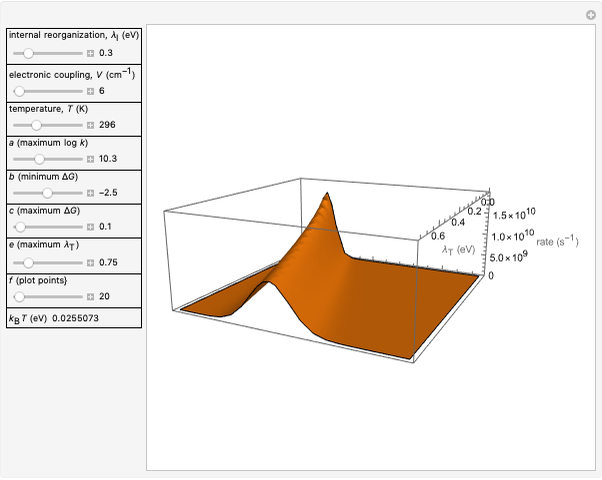
Snapshot 2: for 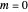 , the semiclassical Marcus equation behaves similarly to the classical Marcus equation
, the semiclassical Marcus equation behaves similarly to the classical Marcus equation
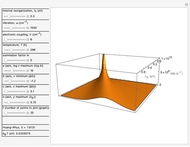
Snapshot 3: in the high temperature limit, the semiclassical Marcus equation reduces to the classical Marcus equation
The results of this Demonstration were checked against the R-package [10] that runs in the statistical software package R [11] for computing and graphics.
References
[1] R. A. Marcus, "Electron Transfer Reactions in Chemistry: Theory and Experiment (Nobel Lecture)," Angewandte Chemie International Edition, 32(8), 1993 pp. 1111–1121. doi:10.1002/anie.199311113.
[2] S. Chaudhuri, S. Hedström, D. D. Méndez-Hernández, H. P. Hendrickson, K. A. Jung, J. Ho and V. S. Batista, "Electron Transfer Assisted by Vibronic Coupling from Multiple Modes," Journal of Chemical Theory and Computation, 13(12), 2017 pp. 6000–6009. doi:10.1021/acs.jctc.7b00513.
[3] P. F. Barbara, T. J. Meyer and M. A. Ratner, "Contemporary Issues in Electron Transfer Research", Journal of Physical Chemistry, 100(31), 1996 pp. 13148–13168. doi:10.1021/jp9605663.
[4] G. L. Closs and J. R. Miller, "Intramolecular Long-Distance Electron Transfer in Organic Molecules," Science, 240(4851), 1988 pp. 440–447. doi:10.1126/science.240.4851.440.
[5] P. Hudhomme and R. M. Williams, "Energy and Electron Transfer in Photo- and Electro-active Fullerene Dyads," Handbook of Carbon Nano Materials (F. D'Souza and K. M. Kadish, eds.), Hackensack, NJ: World Scientific, 2011 pp. 545–591. doi:10.1142/9789814327824_0017.
[6] R. M. Williams. "Introduction to Electron Transfer." (Nov 11, 2021) doi:10.13140/RG.2.2.16547.30244.
[7] R. M. Williams. Photoinduced Electron Transfer—The Classical Marcus Theory [Video]. (Nov 11, 2021) youtu.be/YFzeMMOvhl0.
[8] R. M. Williams. Photoinduced Electron Transfer—The Semi-classical Marcus–Levich–Jortner Theory [Video]. (Nov 11, 2021) youtu.be/GnPIbH6nM9o.
[9] R. M. Williams. University of Amsterdam. (Nov 11, 2021) www.uva.nl/en/profile/w/i/r.m.williams/r.m.williams.html.
[10] J. Idé and G. Raos. "ChargeTransport: Charge Transfer Rates and Charge Carrier Mobilities." (Nov 11, 2021) CRAN.R-project.org/package=ChargeTransport.
[11] "What Is R?" The R Foundation. (Nov 11, 2021) www.r-project.org/about.html.
[12] A. Sarai, "Energy-Gap and Temperature Dependence of Electron and Excitation Transfer in Biological Systems," Chemical Physics Letters, 63(2), 1979 pp. 360–366. doi:10.1016/0009-2614(79)87036-0.
[13] J. R. Miller, J. V. Beitz and R. K. Huddleston, "Effect of Free Energy on Rates of Electron Transfer between Molecules," Journal of the American Chemical Society, 106(18), 1984 pp. 5057–5068. doi:10.1021/ja00330a004.
[14] M. R. Gunner, D. E. Robertson and P. L. Dutton, "Kinetic Studies on the Reaction Center Protein from Rhodopseudomonas sphaeroides: The Temperature and Free Energy Dependence of Electron Transfer between Various Quinones in the QA Site and the Oxidized Bacteriochlorophyll Dimer," Journal of Physical Chemistry, 90(16), 1986 pp. 3783–3795. doi:10.1021/j100407a054.
[15] R. Rujkorakarn and F. Tanaka, "Three-Dimensional Representations of Photo-induced Electron Transfer Rates in Pyrene-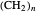 -N,N'-dimethylaniline Systems Obtained by Three Electron Transfer Theories," Journal of Molecular Graphics and Modelling, 27(5), 2009 pp. 571–577. doi:10.1016/j.jmgm.2008.09.008.
-N,N'-dimethylaniline Systems Obtained by Three Electron Transfer Theories," Journal of Molecular Graphics and Modelling, 27(5), 2009 pp. 571–577. doi:10.1016/j.jmgm.2008.09.008.
[16] T. Unger, S. Wedler, F.-J. Kahle, U. Scherf, H. Bässler and A. Köhler, "The Impact of Driving Force and Temperature on the Electron Transfer in Donor–Acceptor Blend Systems," The Journal of Physical Chemistry C, 121(41), 2017 pp. 22739–22752. doi:10.1021/acs.jpcc.7b09213.
[17] W. W. Parson, "Generalizing the Marcus Equation," The Journal of Chemical Physics, 152(18), 2020 184106. doi:10.1063/5.0007569.
[18] J. B. Kelber, N. A. Panjwani, D. Wu, R. Gómez-Bombarelli, B. W. Lovett, J. J. L. Morton and H. L. Anderson, "Synthesis and Investigation of Donor–Porphyrin–Acceptor Triads with Long-Lived Photo-Induced Charge-Separate States", Chemical Science, 6, 2015, pp. 6468-6481. doi:10.1039/C5SC01830G.
[19] G. Lanzani, "Charge Transfer and Transport," The Photophysics behind Photovoltaics and Photonics, Weinheim: Wiley-VCH, 2012 pp. 145–176. doi:10.1002/9783527645138.ch8.
[20] R. M. Williams. Marcus Waves 5 Fast [Video]. (Nov 30, 2021) youtu.be/xn1_2w6-gqs.
[21] R. M. Williams. Marcus Waves 3 Fast [Video]. (Nov 30, 2021) youtu.be/c_Qb89Zvc3s.
Permanent Citation