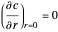Mass Transfer with Reaction in a Spherical Drop

Consider a spherical drop of nonreacting fluid . Species absorbs and diffuses into the interior of the drop and then reacts with the liquid. Assume that the kinetics for this reaction are , where is the reaction order.

The concentration of species is taken to be a function of only. Here, is the radial position, is the drop's radius, is the diffusion coefficient, is the convective heat transfer coefficient, is the concentration of species , is the reaction rate constant, and is the reaction order. The boundary value problem is (BC means boundary condition, IC means initial condition):

, ,

IC: ,

BC1: ,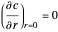

BC2: at .

BC2 defines the mass transfer flux across the interface of the drop and is the far field concentration.

For the analysis we define the following dimensionless variables:

, , ,

where, , , and are the dimensionless concentration, radial position, and time, respectively.

In dimensionless form the PDE becomes:

, (1)

IC: ,

BC1: ,

BC2: at .

The problem then depends on two dimensionless quantities: (i.e. the Sherwood number for mass transfer) and (i.e. the Damköhler number). represents the relative importance of convective mass transport to diffusional transport. When convective transport dominates diffusional transport (i.e. ), the concentration gradients in the drop are negligible. For small Sherwood numbers, the concentration in the drop is governed by diffusional processes. When , one recovers the case when there is no reaction.

We solve the dimensionless form of the problem using the method of lines. Note the problem is linear and the only issue we need to address is the apparent singularity at . Evaluating the limiting behavior at shows that the appropriate equations are

, for ,

, at .

The central difference template for the spatial derivatives of our PDE at the 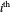node is

, ,

, ,

where we have defined the node spacing by: .

For our problem, we subdivide the drop radius into a grid of intervals such that the grid coordinates are , where . With this definition it follows that and .

The PDE can then be expressed as:

(2)

, (3)

Thus we have equations in unknowns. At we have the following BC:

.

Approximating the spatial derivative with a central difference gives

.

Solving for gives:

, (4)

while at we have

;

a central difference formula gives

, (5)

where is evaluated at ξ =ξ₁-Δξ=-Δξ. Thus equations (4) and (5) allow us to eliminate the fictitious nodes from equations (2) and (3) to give equations in terms of unknown values.

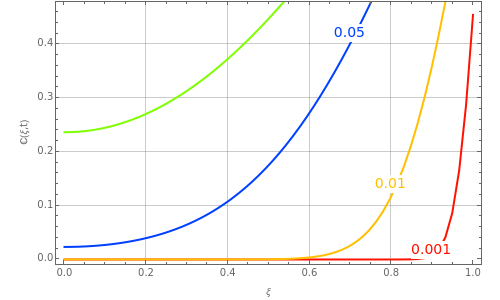
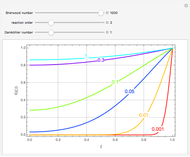
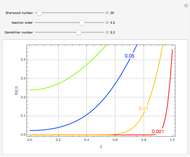
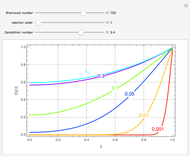
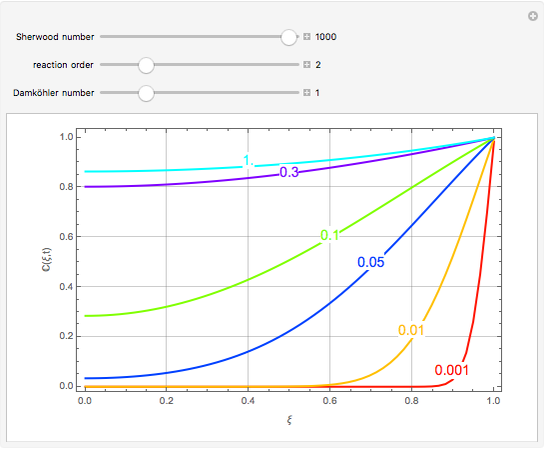
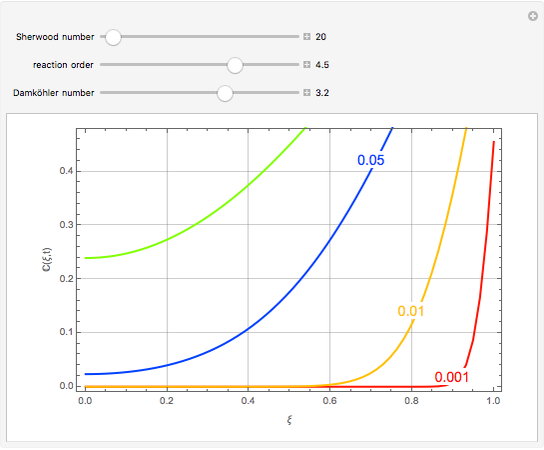
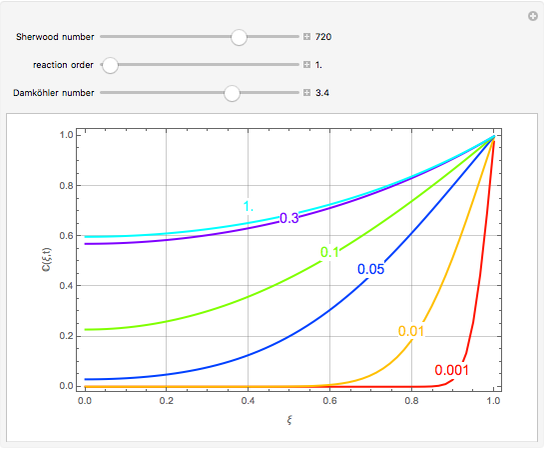
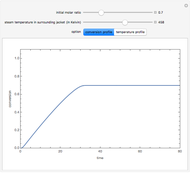
This Demonstration plots the concentration profile versus the radial position, , for several values of the dimensionless time, . You can vary the Sherwood number, the reaction order (e.g. is a first-order reaction), and the Damköhler number (e.g. or no chemical reaction, see the last snapshot). For large values of , the boundary condition BC2 becomes .