Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Mazes on Nets of Rhombic Dodecahedra

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

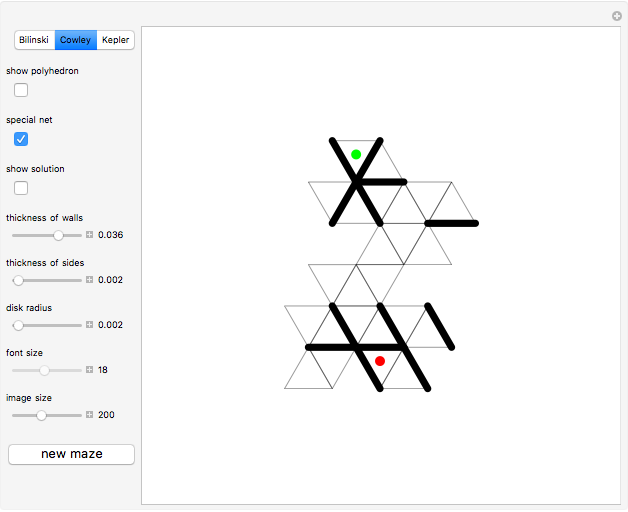
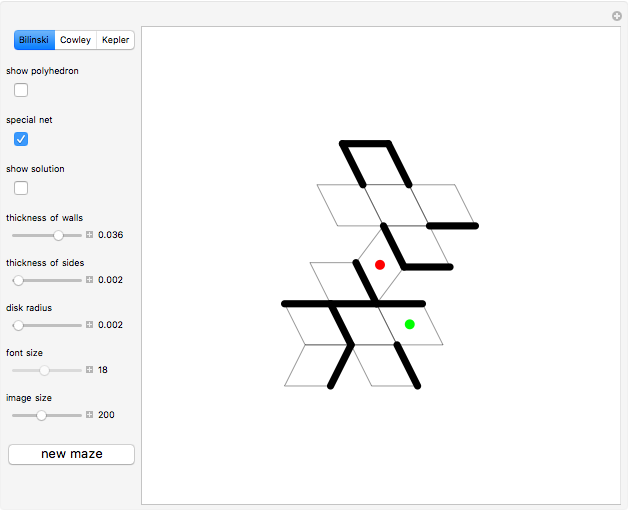
First, select a polyhedron: Bilinski, Cowley or Kepler. With "show polyhedron" off, find the shortest path from the face with the green dot to the face with the red dot. Cowley's dodecahedron is a nonconvex solid that can be folded from the net of a dodecarhombus [1]; it consists of 24 equilateral triangles partitioned in pairs that form skew rhombuses.

[more]

In [2, pp. 2–3] and [3, p. 22], it was shown that Cowley's dodecarhombus net [1] did not consist of golden rhombuses (like Bilinski's) nor of rhombuses of a rhombic dodecahedron (like Kepler's), so it cannot be folded into a convex polyhedron, but if we consider Cowley's rhombuses as hinged equilateral triangles, the net can be folded into a nonconvex polyhedron. So in this case, rhombuses are a kind of skeleton in the sense of [4, p. 282], although not all dihedral angles are congruent.

[less]

Contributed by: Izidor Hafner (January 2019)
Open content licensed under CC BY-NC-SA

Details

There is an extensive discussion of Cowley's dodecarhombus net in [5, pp. 76–80]. The net of a rhombic dodecahedron of the second kind (Bilinski's dodecahedron) in [2, p. 3] was made by Hafner and was part of an internet discussion mentioned in [3, p. 22], where it supported Hafner's claim that Cowley's net was not a net of a rhombic dodecahedron of the second kind.

References

[1] J. L. Cowley, Geometry Made Easy: A New and Methodical Explanation of the Elemnets [sic] of Geometry, London: Mechell, 1752. www.library.gatech.edu/mensuration/plates1_frame.htm, www.library.gatech.edu/mensuration/build1_frame.htm.

[2] "Rombski poliedri." (Jan 10, 2019) www.logika.si/revija/Stare-revije/revija15-5.pdf.

[3] B. Grünbaum. "The Bilinski Dodecahedron, and Assorted Parallelohedra, Aonohedra, Monohedra, Isozonohedra and Otherhedra." (Jan 10, 2019) digital.lib.washington.edu/researchworks/bitstream/handle/1773/15593/Bilinski_dodecahedron.pdf.

[4] P. R. Cromwell, Polyhedra, New York, NY: Cambridge University Press, 1997.

[5] M. Friedman, A History of Folding in Mathematics: Mathematizing the Margins, New York, NY: Springer Berlin Heidelberg, 2018.

Snapshots
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send