Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Mechanism for Drawing a Logarithmic Spiral

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

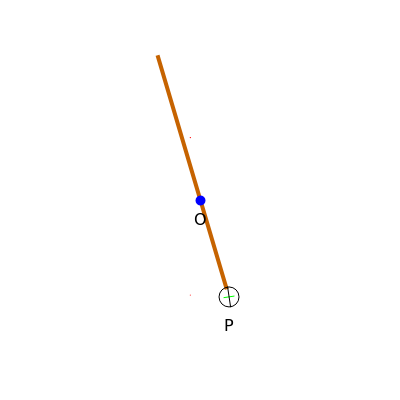
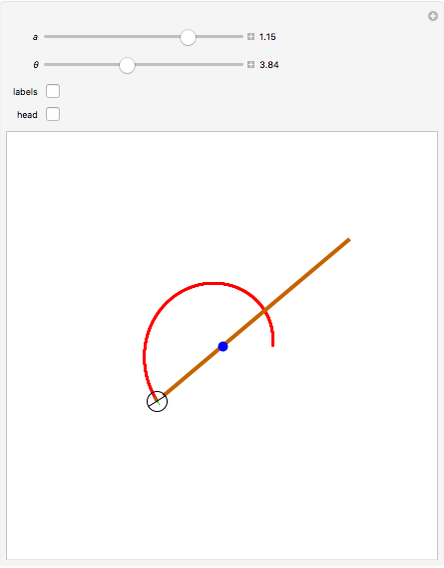
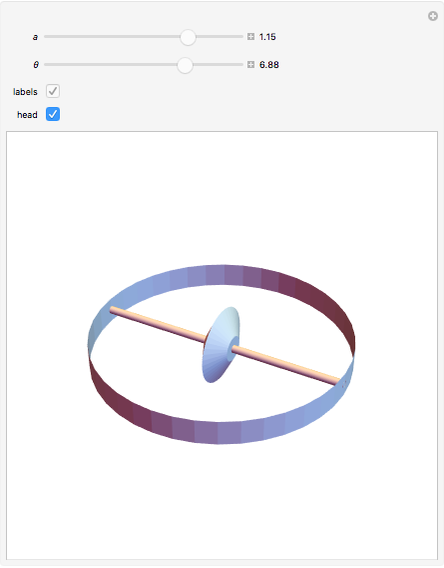
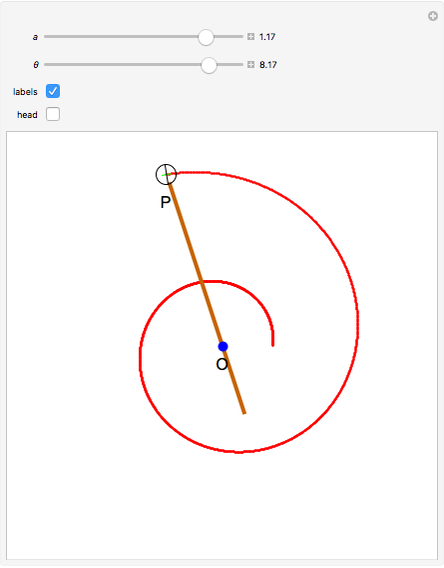
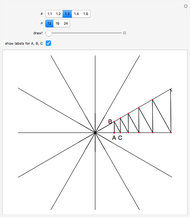
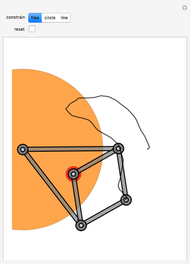
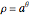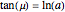This Demonstration shows a mechanism for drawing a logarithmic spiral . A pivot point holds a rod with a sharp wheel at the far end. The axis of the wheel is at an angle to the rod; is chosen such that . As the wheel digs into the plane, it gradually pulls away from the pivot point and traces the spiral.

Contributed by: Izidor Hafner (January 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

For 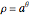, the derivative with respect to is 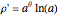. For the angle between the radius vector to a point 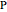and its tangent, we have . For the angle , we have . (If , the curve is a circle; as , the curve tends to the straight line .)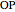

Reference

[1] A. A. Savelov, Plane Curves (in Croatian), Zagreb: Školska knjiga, 1979 p. 265.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send