Model for Earthquake on a Tall Building

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
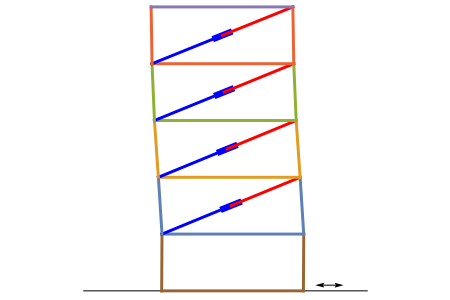
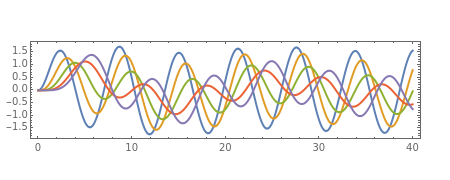
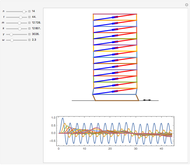
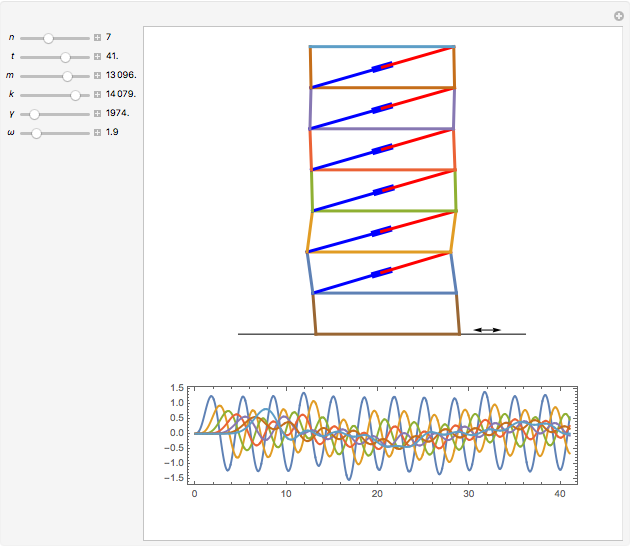
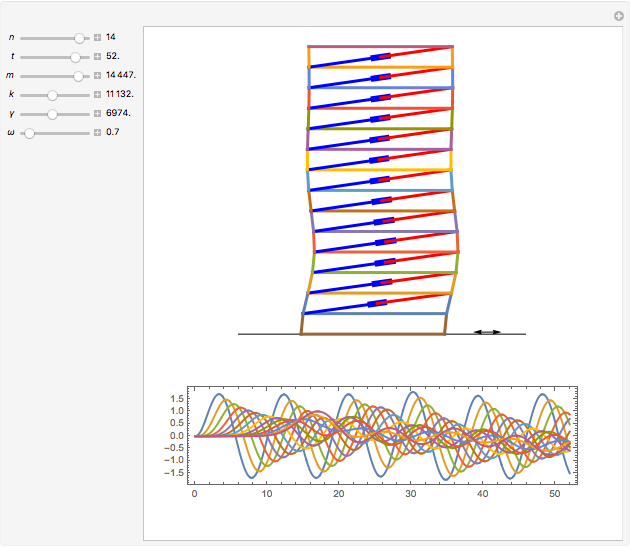
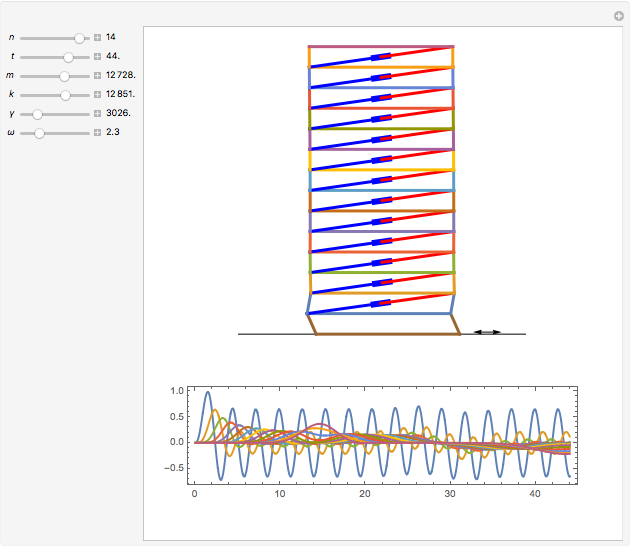
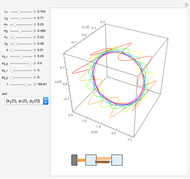
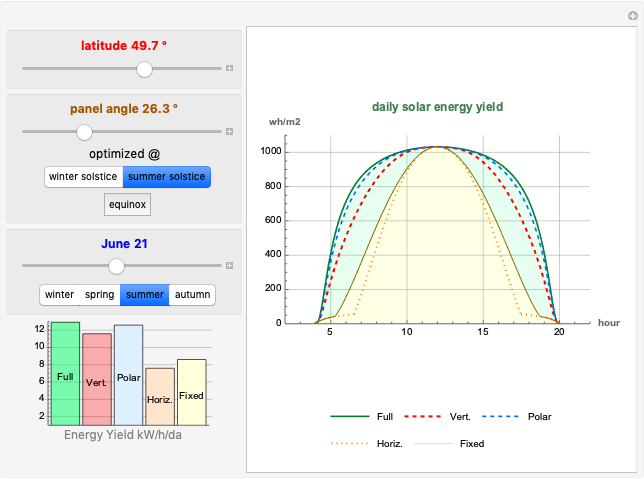
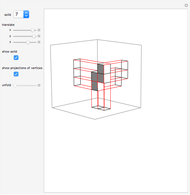
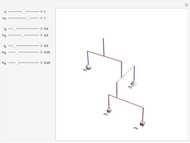
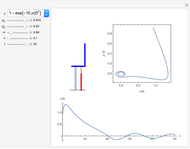
This is a rough model of the behavior of an idealized tall building undergoing horizontal seismic motion. The building has  floors supported by walls. (Each floor has mass
floors supported by walls. (Each floor has mass  but the weight is not taken into account.) The displacements of the floors from their equilibrium positions are
but the weight is not taken into account.) The displacements of the floors from their equilibrium positions are  ,
,  , …,
, …,  ; initially these displacements and their velocities are set to zero. Each floor experiences a restoring forces from its contiguous floors according to Hooke's law with a spring constant
; initially these displacements and their velocities are set to zero. Each floor experiences a restoring forces from its contiguous floors according to Hooke's law with a spring constant  . The diagonal lines represent shock absorbers that introduce a damping factor
. The diagonal lines represent shock absorbers that introduce a damping factor  .
.
Contributed by: Enrique Zeleny (January 2013)
With thanks to Franz Brandhuber.
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equation of motion for the  floor is
floor is

 .
.
The equation for the first floor is
 ,
,
where  is the function that represents the motion of the ground, which in this case is of the form
is the function that represents the motion of the ground, which in this case is of the form  .
.
For the  floor,
floor,
 .
.
Reference
[1] J. R. Brannan and W. E. Boyce, Differential Equations: An Introduction to Modern Methods and Applications, 2nd ed., New York: John Wiley & Sons, 2011 pp. 466–468.
Permanent Citation