Mohr's Circle and Stress Transformations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
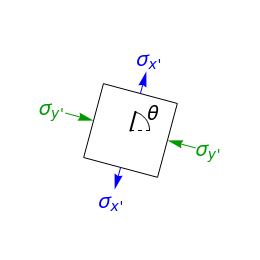
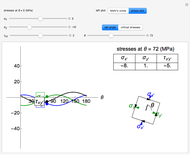
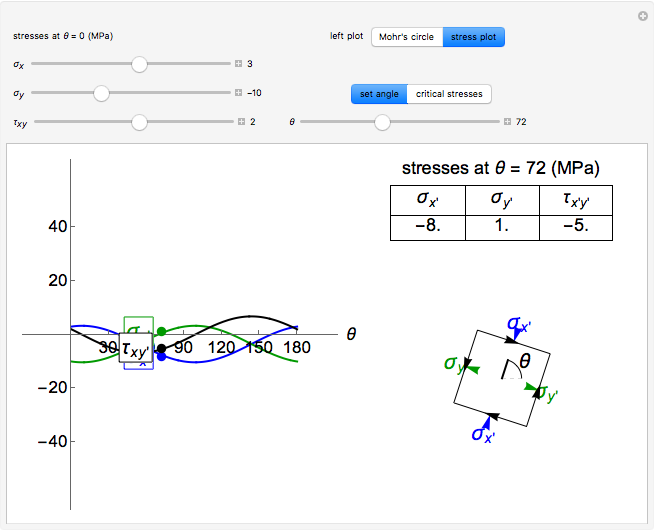
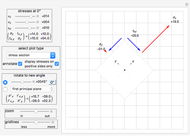
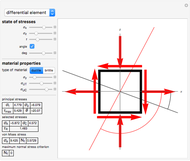
This Demonstration uses a Mohr’s circle and a stress plot to show the effects of stress transformation on a differential element or area. Use sliders to vary the stresses 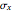 ,
, 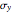 and
and 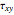 , which correspond to the stresses on the differential element at
, which correspond to the stresses on the differential element at 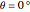 (dashed black line). Select "set angle" to vary the angle
(dashed black line). Select "set angle" to vary the angle  with a slider. Stress transformation equations are used to compute the transformed stresses
with a slider. Stress transformation equations are used to compute the transformed stresses 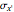 ,
, 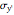 and
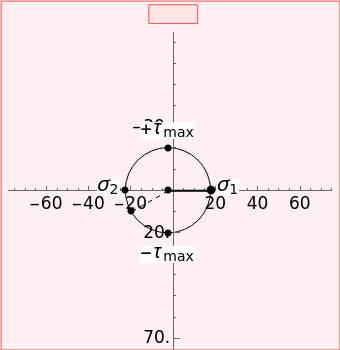
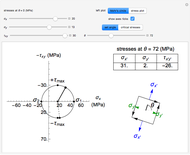
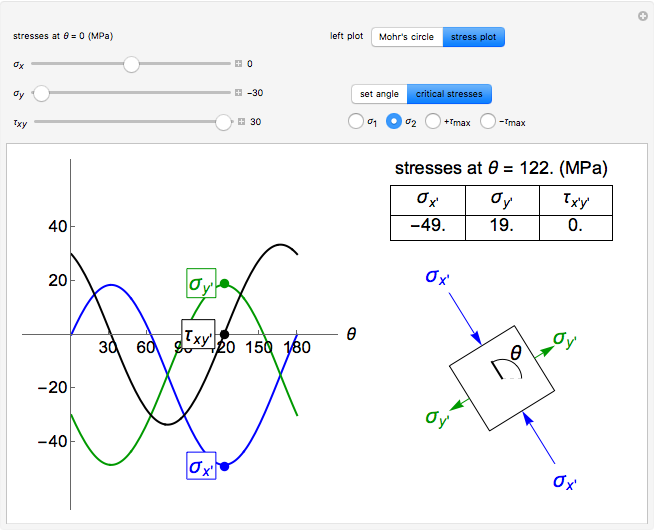
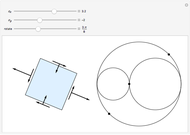
and 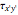 (solid black line), which are shown on the differential stress element as blue, green and black arrows, respectively. Select the "Mohr's circle" button to display Mohr's circle on the left. An angle of
(solid black line), which are shown on the differential stress element as blue, green and black arrows, respectively. Select the "Mohr's circle" button to display Mohr's circle on the left. An angle of  on the differential stress element corresponds to an angle of
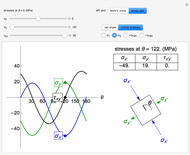
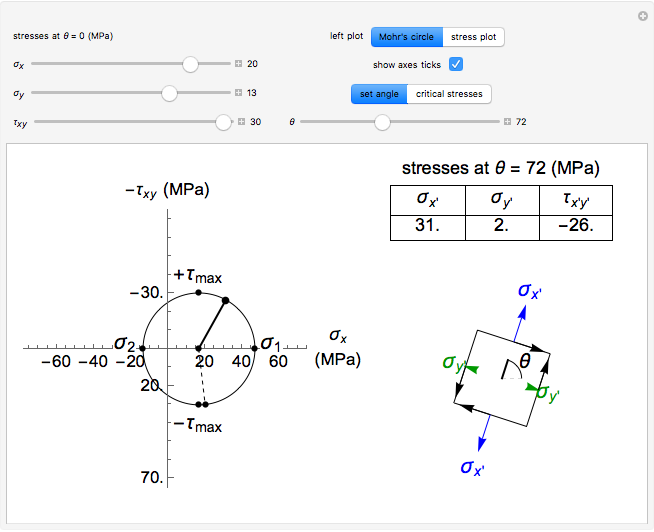
on the differential stress element corresponds to an angle of  on the Mohr's circle. Select the "stress plot" button to display a plot of all three transformed stresses versus
on the Mohr's circle. Select the "stress plot" button to display a plot of all three transformed stresses versus  on the left. Select "set angle" to set
on the left. Select "set angle" to set  with a slider or "critical stresses" to snap the diagram to the angle of one of the principal stresses (
with a slider or "critical stresses" to snap the diagram to the angle of one of the principal stresses ( and
and 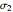 ) or one of the maximum in-plane shear stresses (
) or one of the maximum in-plane shear stresses (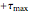 and
and 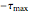 ). Note that Mohr’s circle is displayed with positive
). Note that Mohr’s circle is displayed with positive 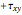 in the downward direction, so an increase in
in the downward direction, so an increase in  results in a counterclockwise rotation on both the Mohr's circle and the differential stress element.
results in a counterclockwise rotation on both the Mohr's circle and the differential stress element.
Contributed by: Nick Bongiardina (October 2016)
Additional contributions by: Jeffery Knutsen, Rachael L. Baumann and John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The transformed stresses are calculated from the normal stresses at 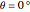 :
:
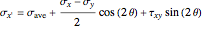 ,
,
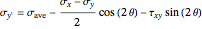 ,
,
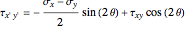 ,
,
where 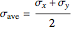 is the average of the
is the average of the  and
and 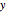 stresses,
stresses, 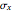 and
and 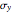 are the normal stresses in the
are the normal stresses in the  and
and 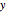 directions and
directions and 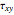 is the shear stress (MPa) at
is the shear stress (MPa) at 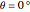 . Here
. Here  is the angle of rotation (positive in the counterclockwise direction),
is the angle of rotation (positive in the counterclockwise direction), 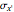 and
and 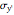 are the normal stresses in the
are the normal stresses in the  and
and 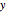 directions (MPa) and
directions (MPa) and 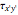 is the shear stress (MPa).
is the shear stress (MPa).
The principal stresses occur for 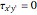 :
:
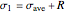 ,
,
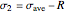 ,
,
 ,
,
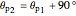 ,
,
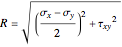 ,
,
where  and
and 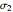 are the first and second principal stresses (MPa),
are the first and second principal stresses (MPa), 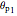 and
and 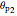 are the first and second principal angles and
are the first and second principal angles and  is the radius of Mohr's circle (MPa). By convention, the right-hand principal stress on the Mohr's circle is denoted as
is the radius of Mohr's circle (MPa). By convention, the right-hand principal stress on the Mohr's circle is denoted as  .
.
The maximum in-plane shear stress is 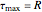 and the maximum shear angle is
and the maximum shear angle is 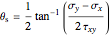 .
.
Reference
[1] R. C. Hibbeler, Statics and Mechanics of Materials, 4th ed., Upper Saddle River, NJ: Pearson, 2014.
Permanent Citation