Mondrian Puzzles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
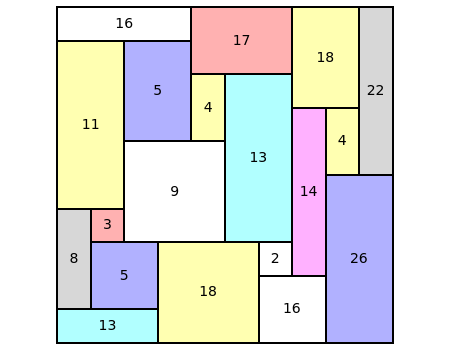
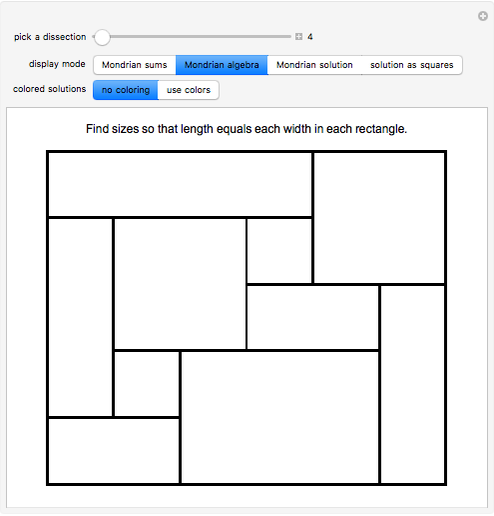
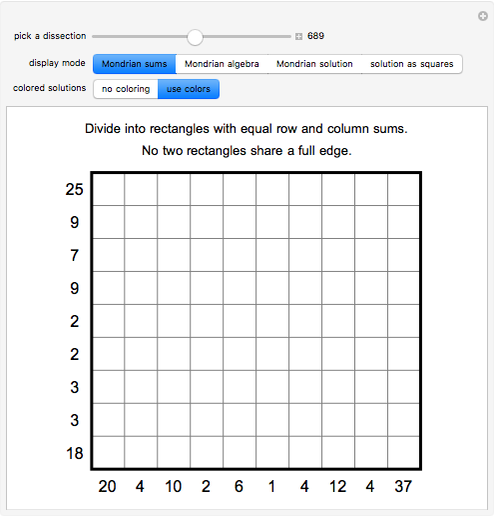
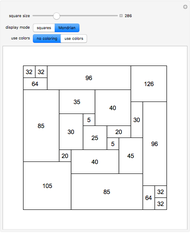
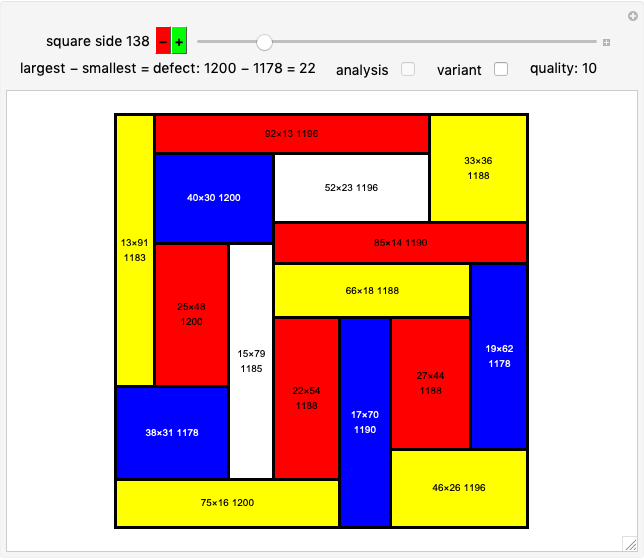
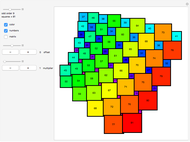
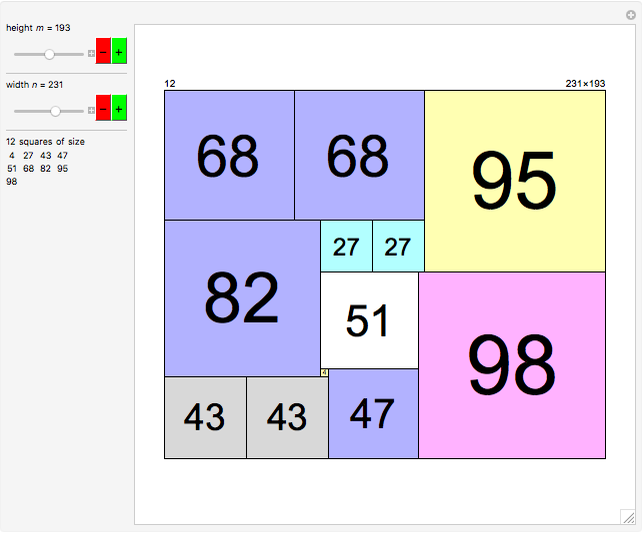
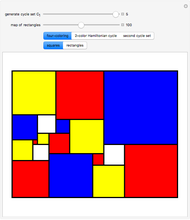
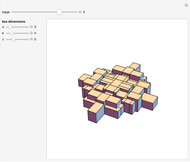
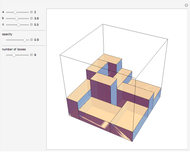
An integer-sided rectangle can always be dissected into squares. Sometimes, a dissection exists where no two squares share a full edge, often called a nowhere-neat dissection.
[more]
Contributed by: Ed Pegg Jr (July 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Ed Pegg Jr, "Mathematical Games: Square Packings," Dec. 1, 2003.
Permanent Citation
"Mondrian Puzzles"
http://demonstrations.wolfram.com/MondrianPuzzles/
Wolfram Demonstrations Project
Published: July 8 2010