Monge Point of a Tetrahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
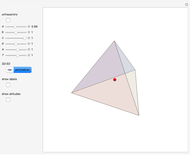
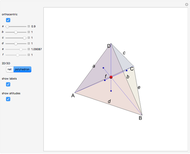
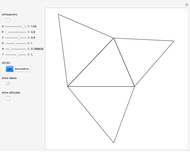
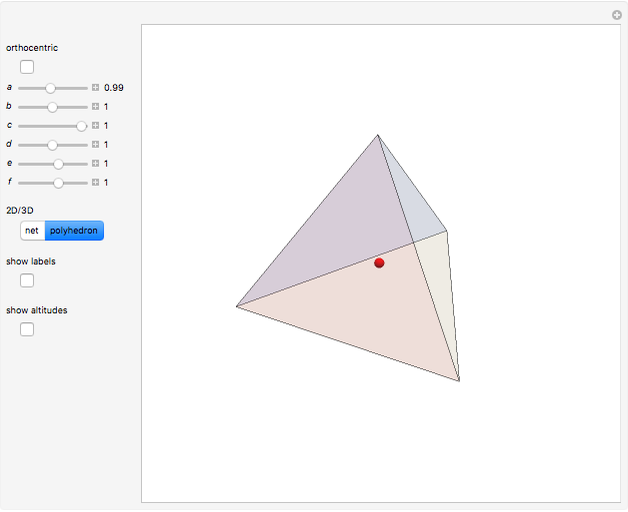
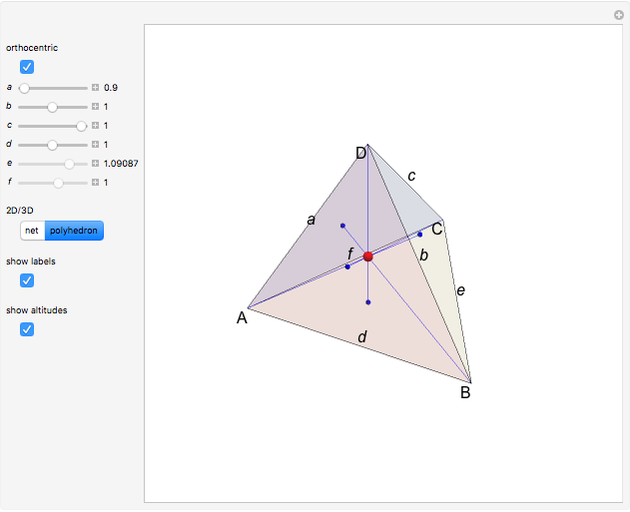
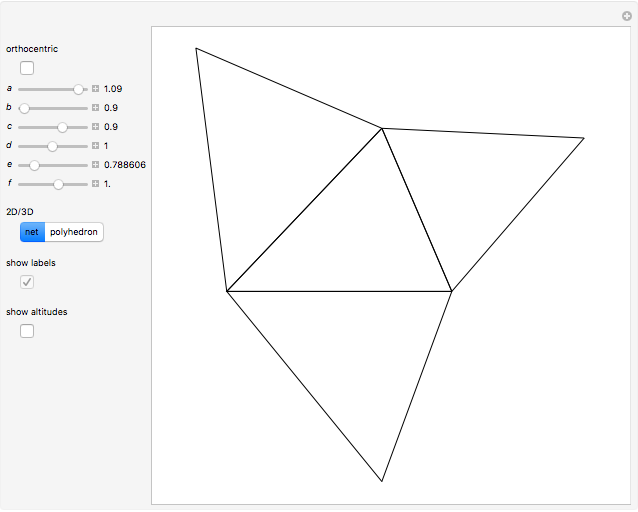
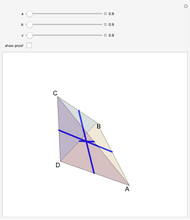
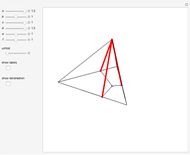
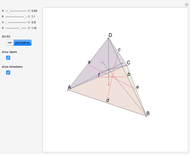
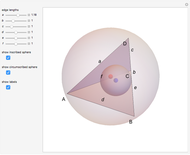
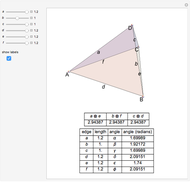
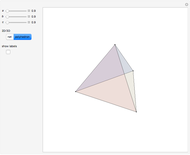
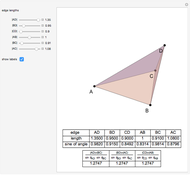
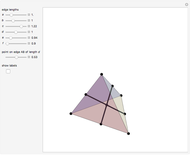
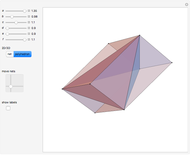
A Monge plane of a tetrahedron is a plane through the midpoint of an edge and perpendicular to the opposite edge. Monge proved that the six Monge planes intersect at a point, known as the Monge point.
[more]
Contributed by: Izidor Hafner (April 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The proof can be found in [1, p. 135].
Reference
[1] V. V. Prasolov and I. F. Sharygin, Problems in Stereometry (in Russian), Moscow: Nauka, 1989.
Permanent Citation
"Monge Point of a Tetrahedron"
http://demonstrations.wolfram.com/MongePointOfATetrahedron/
Wolfram Demonstrations Project
Published: April 25 2017