Nash Equilibria in 3×3 Games

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
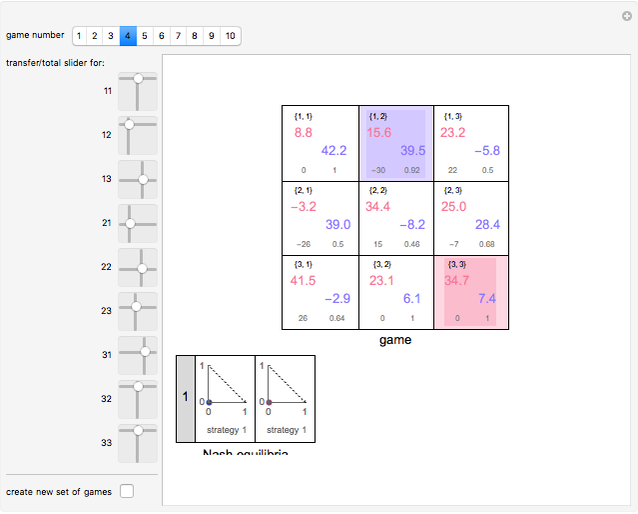
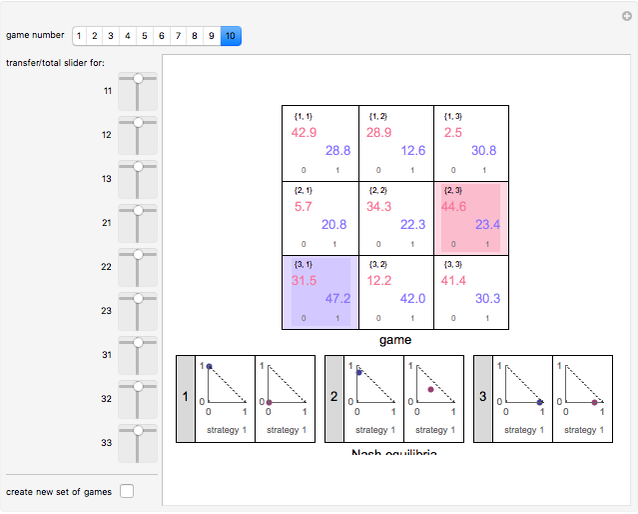
The lower part of the result identifies the Nash equilibria of this game with a sequence of numbered grids containing three pieces of data: (1) an index of the Nash equilibrium in question; (2) a simplex showing the probability that the red player will play strategy 1 or strategy 2; and (3) a simplex showing the probability that the blue player will play strategy 1 or strategy 2. The residual probabilities that each player will play strategy 3 can be calculated from this data. You can transfer wealth between players for each strategy combination or decrease the total wealth available from each strategy combination to see how these modifications of the game affect the Nash equilibria.
Contributed by: Seth J. Chandler (March 2011)
Based on a program by: John Dickaut and Todd Kaplan
Open content licensed under CC BY-NC-SA
Snapshots
Details
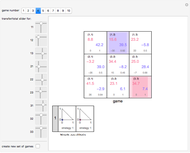
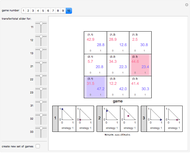
The top panel contains a 3×3 grid in which each cell corresponds to a strategy combination. The strategy combination is identified in small type in the top left of each cell. The payoffs to the red and blue players are shown in red and blue. Small type at the bottom reflects the setting of the associated 2D slider, with the first number showing how much wealth the red player has transferred to the blue player and the second slider showing the fraction of original wealth available. Cells reflecting strategy combinations that constitute a pure Nash equilibrium are colored a light red. The cell reflecting the strategy combination that maximizes total wealth is colored blue, unless it is also a Nash equilibrium, in which case it is colored green.
In real world settings, the interaction of two players often produces payoffs for each. A driver and a pedestrian, for example, may each choose strategies for navigating an intersection. A promisor and a promisee in a contractual relationship may each choose strategies with respect to performance or reliance. One can think of legal rules as altering the payoffs otherwise received by players for various strategy combinations, transferring wealth via the tort system or contract law, for example, in the event one player selects an unduly risky strategy or fails to honor a contract. A useful exercise is to see how one can devise legal rules that transfer wealth from one player to another or that destroy wealth for various strategy combinations in such a fashion as to make the strategy combination that maximizes total wealth correspond to the only pure Nash equilibrium in the game. In this fashion, the greed of the individual players is harnessed so that their private optimization decisions also happen to maximize total wealth. This Demonstration permits such an exploration to be undertaken for a variety of games.
The code for computing the Nash equilibria is taken from a package placed on MathSource, developed by John Dickaut and Todd Kaplan. H. Varian, ed., Economic and Financial Modeling with Mathematica, New York: TELOS/Springer - Verlag, 1993.
Snapshot 1: a modification of game 4 such that the sole Nash equilibrium is a set of pure strategies that also maximizes the total wealth of the players
Snapshot 2: a game in which there are no pure strategy Nash equilibria
Snapshot 3: a game in which the exclusive pure strategy Nash equilibrium does not maximize total wealth
Can you figure out how to use the slider for strategy combination {3,1} to make a wealth conserving transfer between the red and blue players such that the strategy combination that maximizes total wealth becomes the exclusive Nash equilibrium?
Permanent Citation
"Nash Equilibria in 3×3 Games"
http://demonstrations.wolfram.com/NashEquilibriaIn33Games/
Wolfram Demonstrations Project
Published: March 7 2011