Newton-Simpson's Formula for the Volume of a Prismatoid

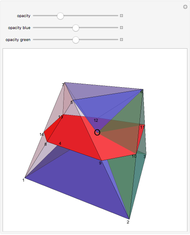
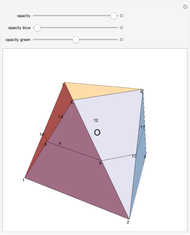
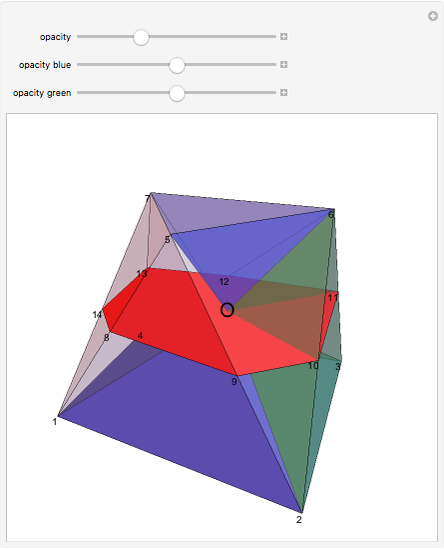
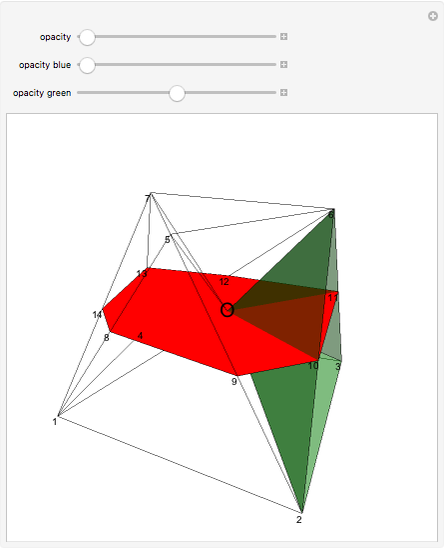
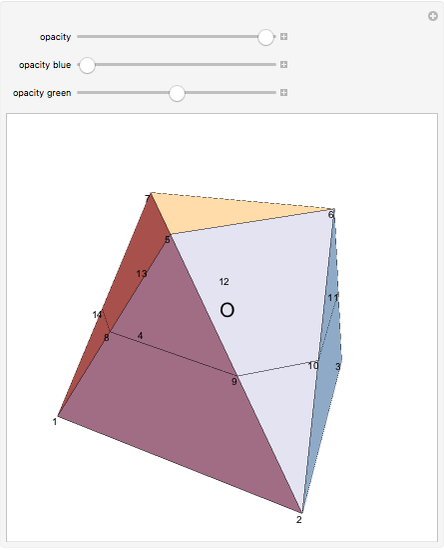
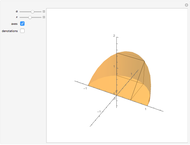
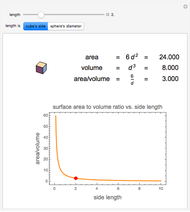
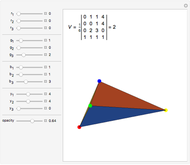
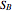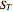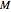A prismatoid is the convex hull of two parallel convex polygons, a base and a top with areas and . Suppose the height of the solid is . Make a cross section at height 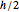, let the point O be on 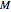, and let the area of 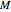be . The sum of the volumes of the two blue pyramids, the first with apex O and base and the other with apex O and base 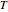, is 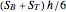. A green pyramid 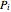with apex O and a side face has volume equal to four times its upper part (the tetrahedron with vertices O, 12, 11, 6). But the volume of this tetrahedron is 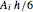, where 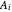is the area of 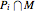. 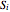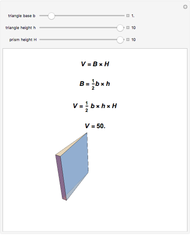The sum of all such areas is 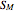. So the volume of the prismatoid is .