Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

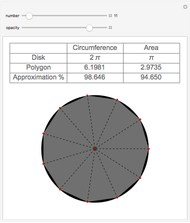
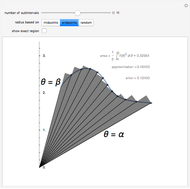
Newton's Pi Approximation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

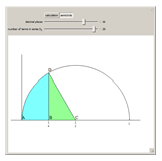
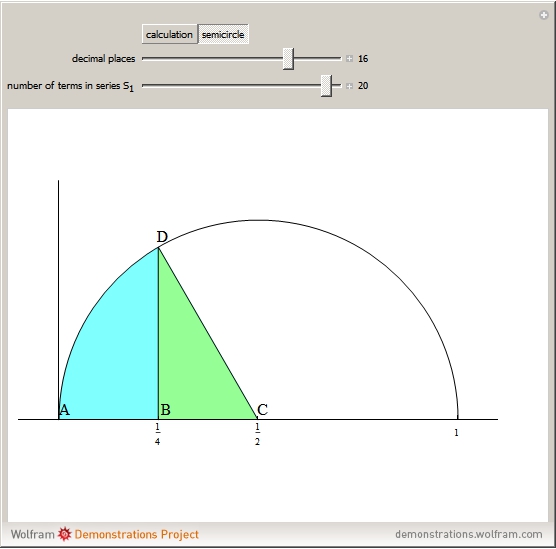
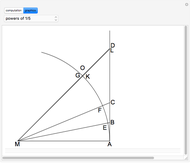
This Demonstration gives Newton's approximation of based on calculating the area of a semicircle using an integral.

[more]

The area under the arc (light blue) is equal to the area of the sector minus the area of triangle (light green), that is, .

On the other hand, the semicircle has equation , so . Set and .

Therefore, .

[less]

Contributed by: Izidor Hafner (August 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

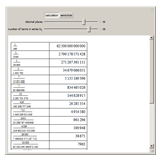
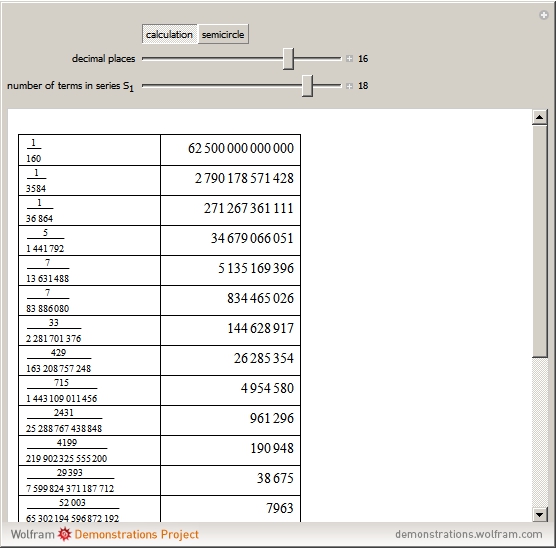
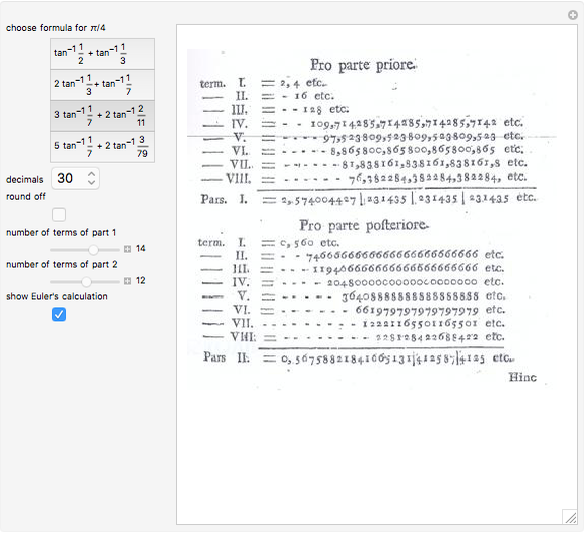
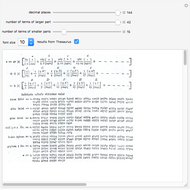
Newton presented to 16 decimal places using 20 terms of the binomial series [1, p. 177].

Reference

[1] W. Dunham, Journey through Genius, New York: Penguin Books, 1990 pp. 174–177.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send