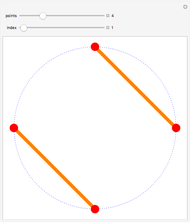
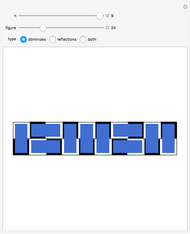
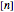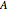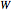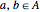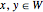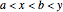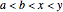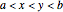Noncrossing Partitions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
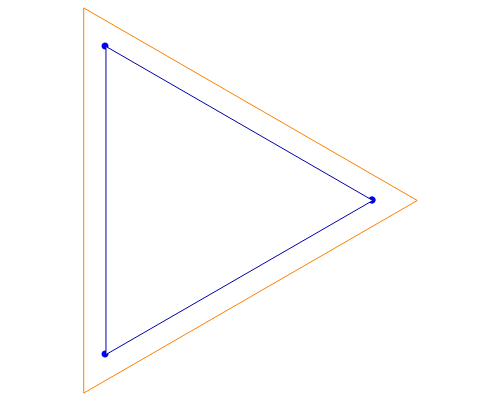
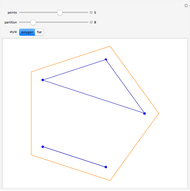
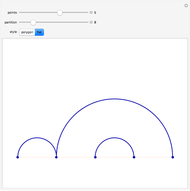
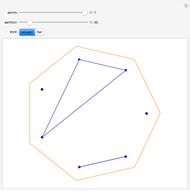
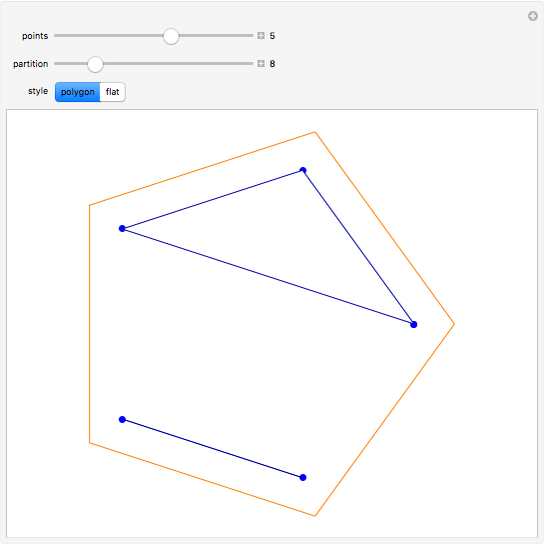
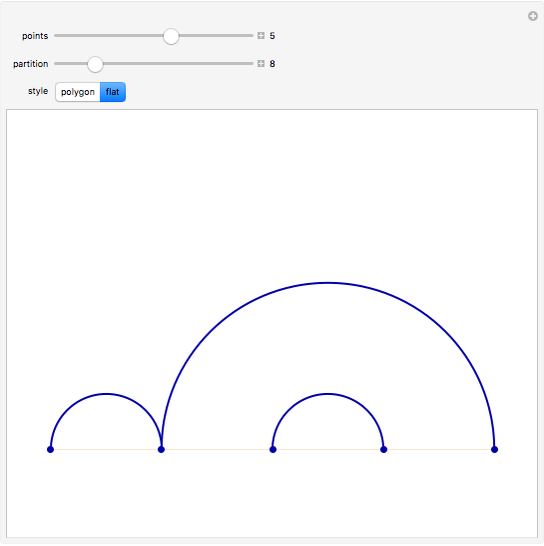
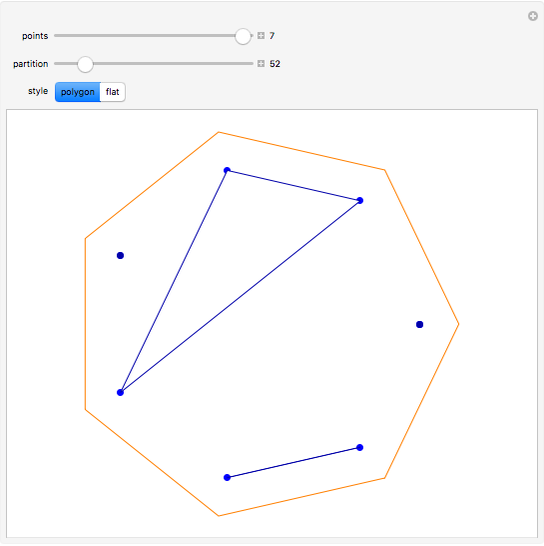
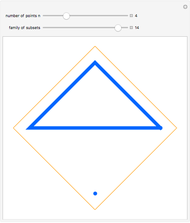
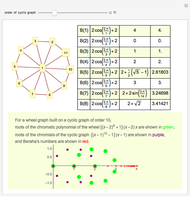
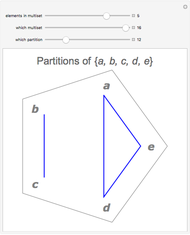
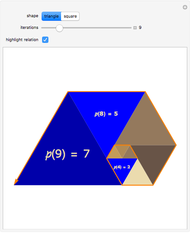
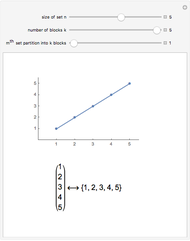
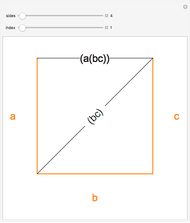
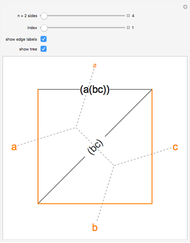
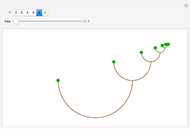
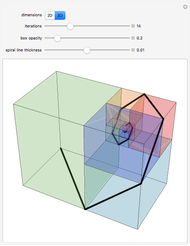
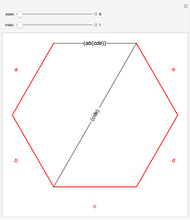
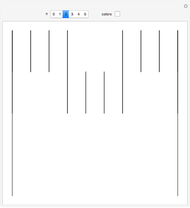
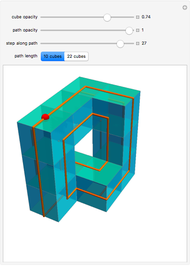
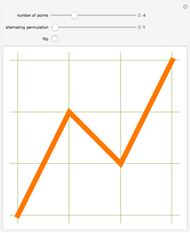
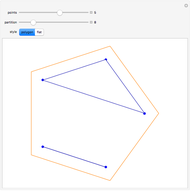
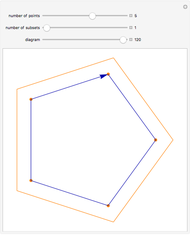
One of the many interpretations of the Catalan numbers 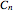 is that they count the number of noncrossing partitions of the set
is that they count the number of noncrossing partitions of the set 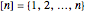 .
.
Contributed by: Robert Dickau (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] R. P. Stanley, Enumerative Combinatorics, Vol. 2, Cambridge: Cambridge University Press, 1999 p. 226.
Permanent Citation