Nonlinear Wave Resonances

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
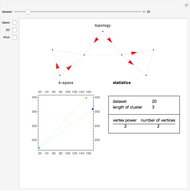
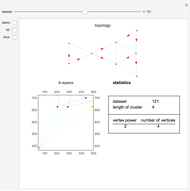
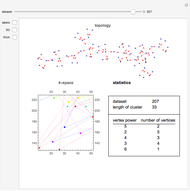
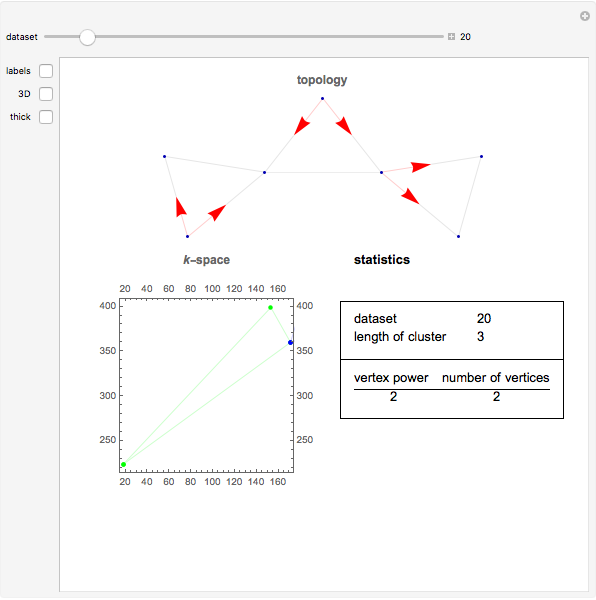
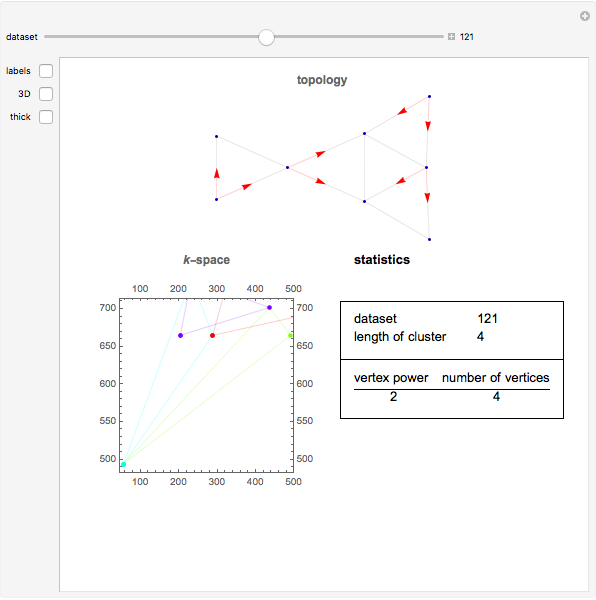
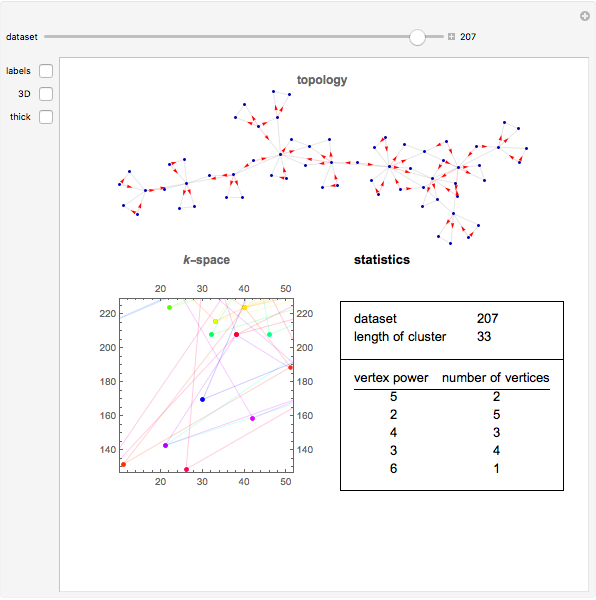
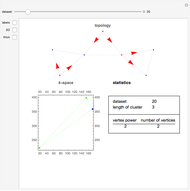
Clustering of three-wave resonances among spherical planetary waves. Top: topological view in the form of a 2D (directed) or 3D graph; bottom: geometrical shape of a cluster in the spectral  -space. Red arrows show the possible directions of the energy flux in a given cluster. Labels designate the coordinates of vertices in the
-space. Red arrows show the possible directions of the energy flux in a given cluster. Labels designate the coordinates of vertices in the  -space.
-space.
Contributed by: Oleksii Rudenko (March 2011)
Suggested by: Elena Kartashova
Open content licensed under CC BY-NC-SA
Snapshots
Details
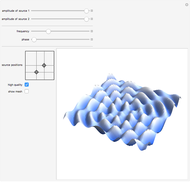
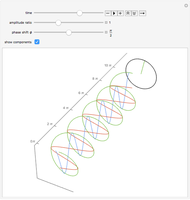
Nonlinear wave resonances play an important role in wave turbulent systems; they are a major mechanism that allows the explanation of many results of laboratory experiments and some real physical phenomena. For instance, three-wave resonances among spherical planetary waves describe so-called intra-seasonal oscillations in the Earth's atmosphere [1]. A very important characteristic of wave systems possessing nonlinear resonances is their ability to form small clusters of waves interacting only among each other.
Knowing the geometrical shape of a cluster in the spectral space (that is, in terms of the coordinates of wavevectors) gives explicit information [2] about the form of dynamical systems corresponding to a given cluster. Notice that for illustrative purposes it is more suitable to use the topological structure of the resonances instead of their geometrical structure. To clarify the point, both presentations—geometrical and topological—are shown for the clusters appearing in the three-wave resonance system of atmospheric planetary waves [1]. The simplest clusters consisting of only three waves (triads) were cut out.
[1] E. Kartashova and V. S. L'vov, "Model of Intraseasonal Oscillations in Earth's Atmosphere," Phys. Rev. Lett., 98(19): 198501, 2007. [2] E. Kartashova and G. Mayrhofer, "Cluster Formation in Mesoscopic Systems," Physica A: Stat. Mech. Appl., 385(2), 2007 pp. 527-542. [3] E. Kartashova and V. S. L'vov, "Triad Dynamics of Planetary Waves," Europhys. Lett. (submitted), e-print: arXiv:0801.3374v1 [nlin.CD], 2008.
Permanent Citation
"Nonlinear Wave Resonances"
http://demonstrations.wolfram.com/NonlinearWaveResonances/
Wolfram Demonstrations Project
Published: March 7 2011