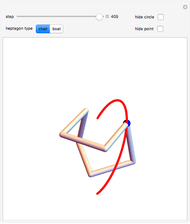
Nonplanar Rectangular Heptagons

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
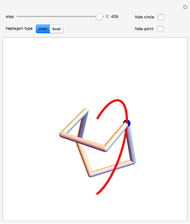
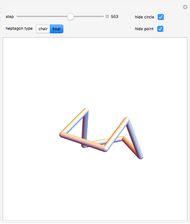
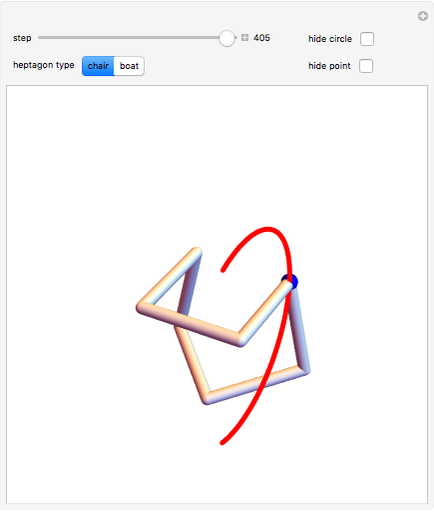
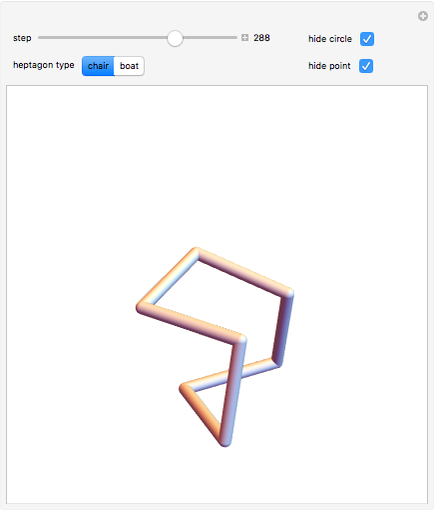
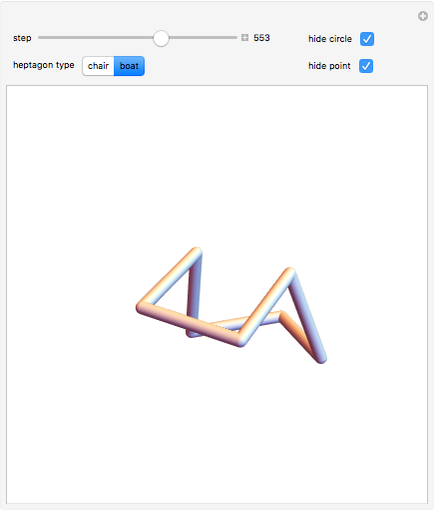
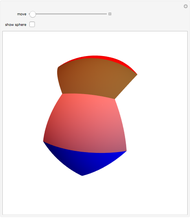
This Demonstration shows two infinite families of nonplanar regular 7-gons in 3-space having a 90° angle at each junction. Each family is parametrized by the points on a circular arc.
Contributed by: Barry Cox and Stan Wagon (July 2013)
(University of Adelaide, Australia, Macalester College, St. Paul, Minnesota, USA)
Open content licensed under CC BY-NC-SA
Details
The existence of a nonplanar regular 7-gon with right angles at each vertex was discovered by Wildenberg [1]. He showed that the only positive integers  for which rectangular regular
for which rectangular regular  -gons do not exist are 1, 2, 3 and 5.
-gons do not exist are 1, 2, 3 and 5.
This appears to be an unresolved question: is there a rectangular regular 7-gon that does not belong in either of these two families?
For a discussion of regular heptagons with common angle  not equal to a right angle, see [2].
not equal to a right angle, see [2].
 ,
,
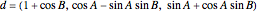 ,
,
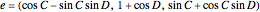 .
.
Now each vector between points is guaranteed to be a unit vector, except for  , so we need only specify that condition and the remaining two right angles as follows:
, so we need only specify that condition and the remaining two right angles as follows:
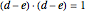 ,
,
 ,
,
 .
.
So when we view this system as having the parameter  and use a specific value such as
and use a specific value such as 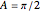 , we find that the solution involves a root of a degree-16 polynomial.
, we find that the solution involves a root of a degree-16 polynomial.
But there appears to not be a general algebraic result, and we can use a numerical technique to obtain two distinct one-dimensional families of solutions. In the first family, where the symmetric instance is known as the chair, the angle  runs from
runs from  to
to 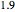 and down to
and down to  and back up to
and back up to  in rough sine-curve form. The second family is based on the boat and has
in rough sine-curve form. The second family is based on the boat and has 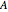 running from
running from  to
to 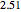 , but it has extra dips, so is more complicated than the simplest wave. We cannot get, physically, from a solution in one family to a solution in the other.
, but it has extra dips, so is more complicated than the simplest wave. We cannot get, physically, from a solution in one family to a solution in the other.
References
[3] G. Wildenberg, "Problem 1110, Seven Is Possible," Mathematics Magazine, 55(1), 1982 pp. 47–48.
Snapshots
Permanent Citation