Normal Curvature at a Regular Point of a Surface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
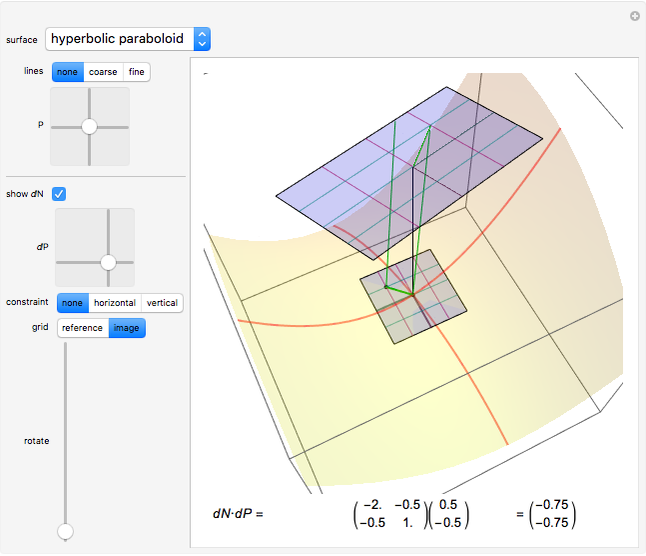
Choose from four types of a regular point on a surface and see how the normal curvature changes as the normal plane rotates around the normal line at this point.
Contributed by: Desana Štambuk (University of Zagreb) (March 2011)
Suggested by: Sonja Gorjanc
Open content licensed under CC BY-NC-SA
Snapshots
Details
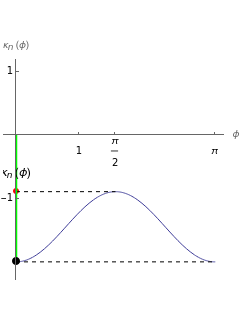
Since the normal curvature  of a surface
of a surface  at a regular point
at a regular point  is a continuous function, it has both a maximum and a minimum on
is a continuous function, it has both a maximum and a minimum on  (according to the extreme value theorem). These extrema are the principal curvatures
(according to the extreme value theorem). These extrema are the principal curvatures  and
and  of
of  at
at  and the Euler curvature formula
and the Euler curvature formula  is valid. If
is valid. If  ,
,  defines the asymptotic direction at
defines the asymptotic direction at  .
.
The Gaussian curvature of  at
at  is defined as
is defined as  .
.
A point  on the surface is called:
on the surface is called:
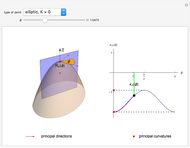
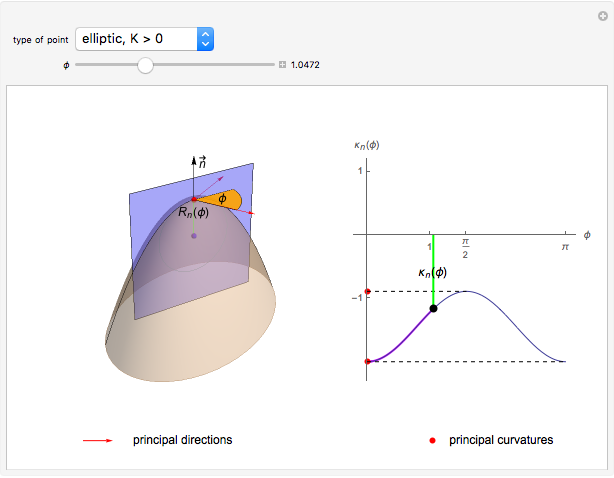
- An elliptic point if  (or the principal curvatures
(or the principal curvatures  and
and  have the same sign). There are no asymptotic directions.
have the same sign). There are no asymptotic directions.
- A hyperbolic point if  (or the principal curvatures
(or the principal curvatures  and
and  have opposite signs). There are exactly two asymptotic directions, and the principal directions bisect the angle between them.
have opposite signs). There are exactly two asymptotic directions, and the principal directions bisect the angle between them.
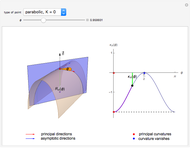
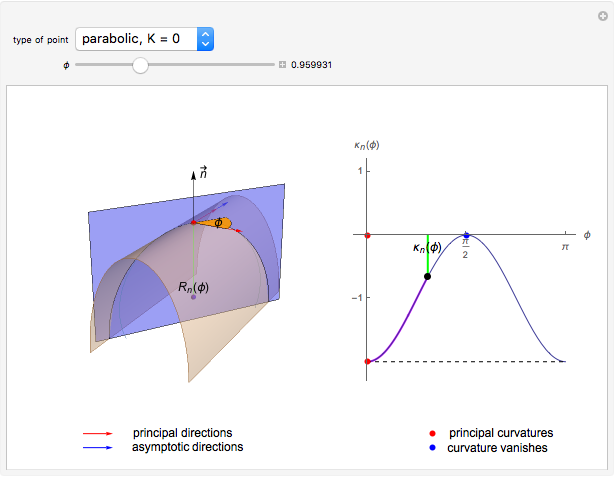
- A parabolic point if  and exactly one of the principal curvatures vanishes.
and exactly one of the principal curvatures vanishes.
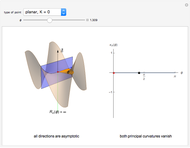
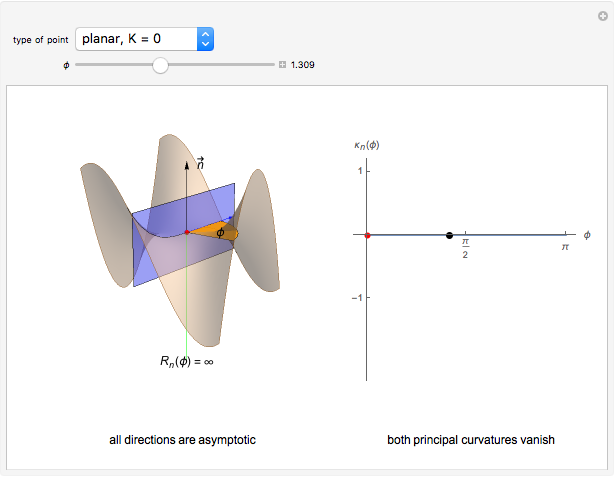
- A planar point if  and both
and both  and
and  vanish—that is, every direction is asymptotic.
vanish—that is, every direction is asymptotic.
Based on work by S. Gorjanc: Gaussian and Mean Curvatures at the Regular Point of a Surface.
Reference:
A. Gray, Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed., Boca Raton: CRC Press LLC, 1998.
Permanent Citation