Normal Forces Can Do Work
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
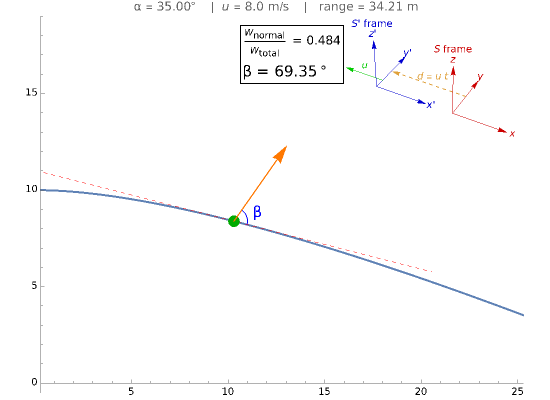
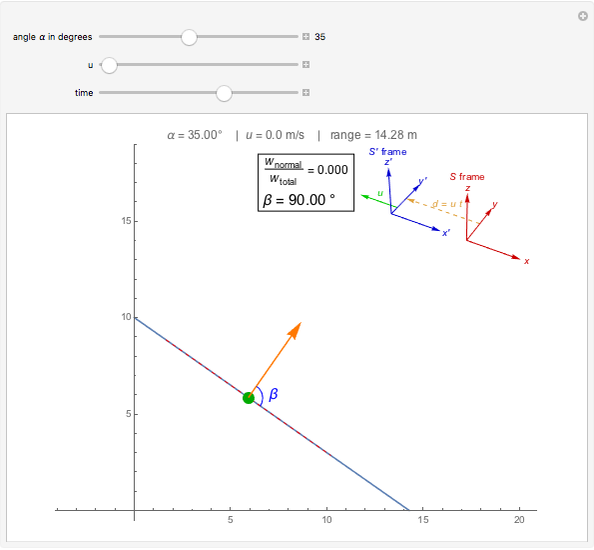
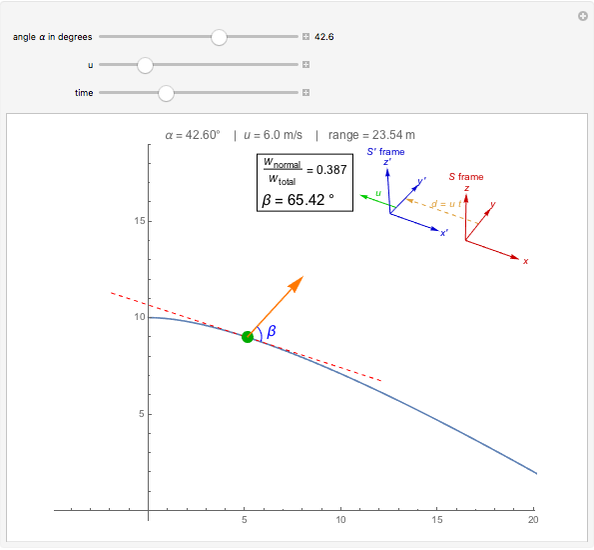
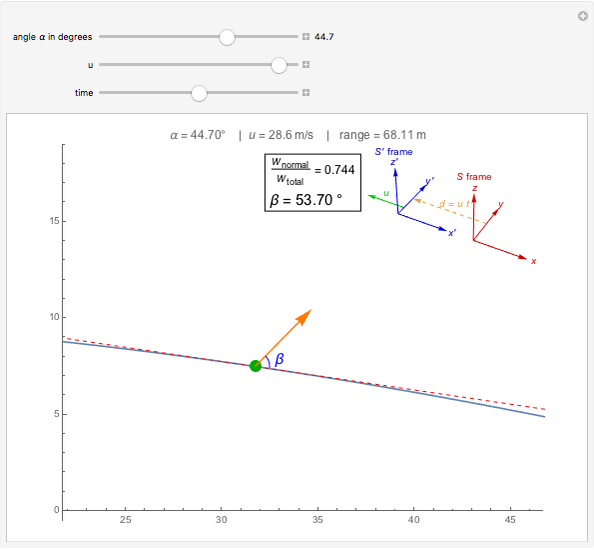
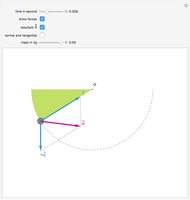
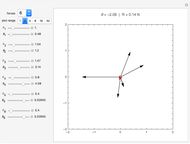
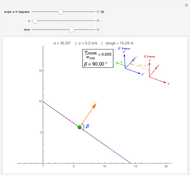
This Demonstration illustrates the fact that a normal force can do work in moving reference frames. A system consisting of a block sliding on a wedge at angle 
is seen in an inertial reference frame 
that moves to the left with speed 
with respect to the reference frame 
in which the block and the wedge are at rest. In 
the normal force is not perpendicular to the trajectory and thus does work. Only in the case of 
, when the normal force is perpendicular to the trajectory, does the work vanish.
Contributed by: Diego A. Manjarres G., Rodolfo A. Diaz S., and William J. Herrera (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This problem shows that the work done by a force depends on the reference frame, and consequently its associated potential energy (if any). When the reference frame changes, some work associated with forces that do no work in the initial frame can appear; in the Galilean case this work is easily evaluated from the net impulse.
It is possible to show the expected Galilean covariance of the work and energy theorem. In the more general case of noninertial translational reference frames, the form of the theorem is preserved as long as the fictitious work is included. Additionally, in the center of mass system the total fictitious work vanishes, even if such a system is noninertial.
For more information, see:
R. A. Diaz, W. J. Herrera, and D. A. Manjarres, "Work and Energy in Inertial and Noninertial Reference Frames," American Journal of Physics, 77(3), 2009 pp. 270–273.
Permanent Citation
"Normal Forces Can Do Work"
http://demonstrations.wolfram.com/NormalForcesCanDoWork/
Wolfram Demonstrations Project
Published: March 7 2011
Mechanical Work
Enrique Zeleny
Pseudo-Forces in a Rotating Reference Frame
Bernard Vuilleumier
Work in an Attractive Inverse-Square Field
Bartosz Naskrecki
Work Is Independent of Path in a Conservative Field
Enrique Zeleny
Forces on a Pendulum
Bernard Vuilleumier
Resultant of a Sum of Forces
Enrique Zeleny
Static Equilibrium and Triangle of Forces
Gianni Di Domenico (Université de Neuchâtel)
Normal Modes of a Double Pendulum
David L. Pincus
Normal Modes of a Beaded String
Enrique Zeleny
Drag and Gravity Forces on a Falling Sphere
Conrad A. Benulis
