Normal Modes of a Double Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
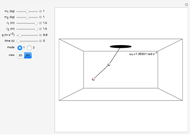
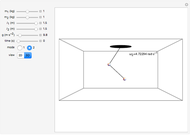
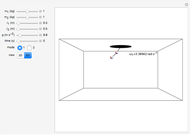
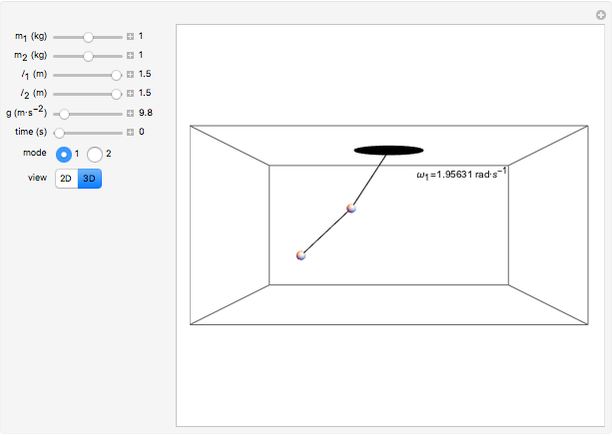
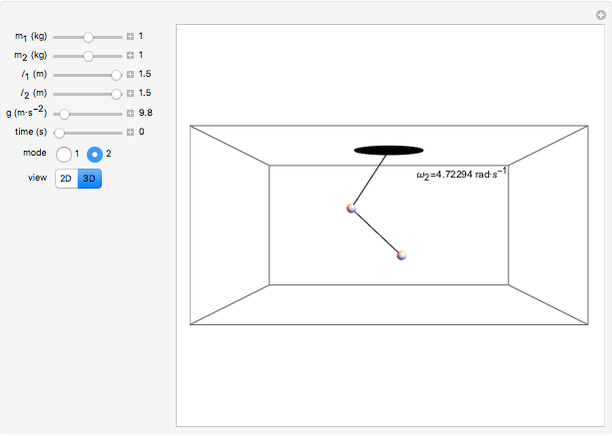
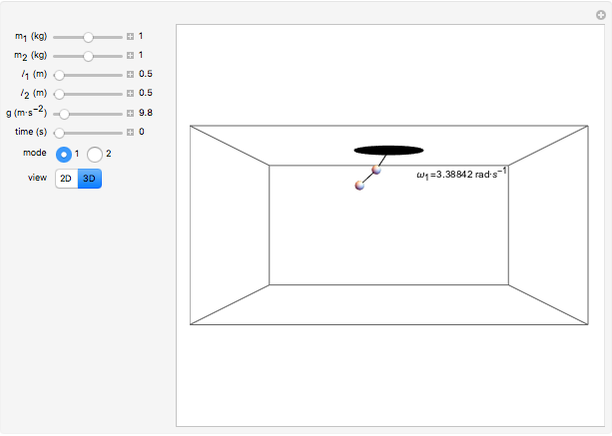
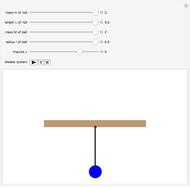
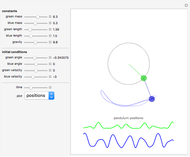
The concept of normal modes of a mechanical system is nicely illustrated by a double pendulum. The normal modes of a mechanical system are single frequency solutions to the equations of motion; the most general motion of the system is a superposition of its normal modes. You can adjust the controls to determine how the masses and lengths of the component pendula affect the normal modes. The symmetric mode of oscillation is always of a lower frequency than the antisymmetric mode of oscillation.
Contributed by: David L. Pincus (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Lagrangian, 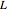 , of the system is given by
, of the system is given by 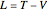 , where
, where 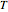 and
and 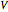 are the kinetic energy and the potential energy of the system. If we choose as our generalized coordinates the set
are the kinetic energy and the potential energy of the system. If we choose as our generalized coordinates the set 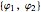 , where
, where 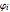 represents the angular displacement of the
represents the angular displacement of the 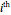 mass from the vertical, then
mass from the vertical, then 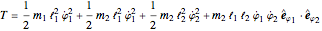 , where
, where 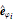 is a unit vector pointing in the direction of increasing
is a unit vector pointing in the direction of increasing  and
and 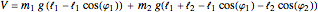 , where
, where  is the acceleration due to gravity, approximately
is the acceleration due to gravity, approximately 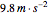 near the surface of the Earth. If
near the surface of the Earth. If 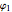 and
and 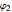 are both small, then
are both small, then 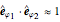 and
and 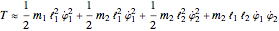 . Similarly, if
. Similarly, if 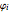 is small, then
is small, then 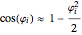 and
and 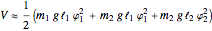 . With these approximations, we can write
. With these approximations, we can write 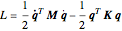 , where
, where 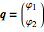 ,
, 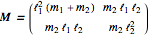 ,
, 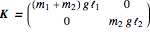 , and all vector and matrix components refer to the standard basis of
, and all vector and matrix components refer to the standard basis of 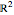 ,
, 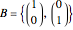 . It is helpful to find a new basis
. It is helpful to find a new basis 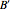 in which both
in which both 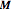 and
and 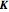 are diagonal. The components of
are diagonal. The components of  in
in 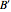 (
(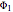 and
and 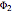 ) are called normal coordinates and it is helpful to consider Lagrange's equations of motion to fully understand their importance.
) are called normal coordinates and it is helpful to consider Lagrange's equations of motion to fully understand their importance. 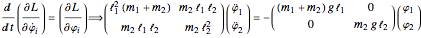 or
or 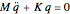 . Thus, the off-diagonal components of
. Thus, the off-diagonal components of 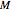 couple the differential equations governing the motions
couple the differential equations governing the motions 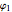 and
and 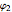 . In the new basis
. In the new basis 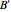 both
both 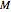 and
and 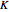 are diagonal and the equation
are diagonal and the equation 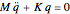 takes the form
takes the form 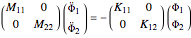 . Thus, the components of
. Thus, the components of  in the new basis
in the new basis 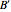 (i.e., the normal coordinates) satisfy a set of homogeneous second order linear differential equations, each of which corresponds to the motion of a simple harmonic oscillator (SHO). To find the basis
(i.e., the normal coordinates) satisfy a set of homogeneous second order linear differential equations, each of which corresponds to the motion of a simple harmonic oscillator (SHO). To find the basis 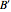 , we substitute a SHO solution of the form
, we substitute a SHO solution of the form 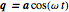 into Lagrange's equations of motion (
into Lagrange's equations of motion (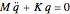 ) and find that
) and find that 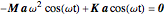 or
or 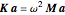 . This generalized eigenvalue equation is tackled by solving the secular equation
. This generalized eigenvalue equation is tackled by solving the secular equation 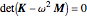 for the eigenvalues
for the eigenvalues 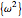 and substituting these values back into
and substituting these values back into 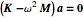 to determine the eigenvectors
to determine the eigenvectors 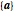 . (Alternatively, we can solve a generalized eigenvalue problem using Mathematica's convenient Eigensystem[{
. (Alternatively, we can solve a generalized eigenvalue problem using Mathematica's convenient Eigensystem[{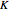 ,
,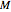 }] command.) The normalized eigenvectors
}] command.) The normalized eigenvectors 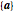 form the new basis
form the new basis 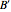 and correspond to the normal modes of motion and the associated eigenvalues correspond to the square of the eigenfrequencies at which the various modes vibrate. In a particular mode all generalized coordinates vibrate with the same frequency (the eigenfrequency, or normal frequency, of the mode), while the corresponding eigenvector provides the amplitude of each generalized coordinate's vibration.
and correspond to the normal modes of motion and the associated eigenvalues correspond to the square of the eigenfrequencies at which the various modes vibrate. In a particular mode all generalized coordinates vibrate with the same frequency (the eigenfrequency, or normal frequency, of the mode), while the corresponding eigenvector provides the amplitude of each generalized coordinate's vibration.
G. R. Fowles and G. L. Cassiday, Analytical Mechanics, 6th ed., Fort Worth: Saunders College Publishing, 1999.
F. W. Byron, Jr. and R. W. Fuller, Mathematics of Classical and Quantum Physics, New York: Dover Publications, 1992.
Permanent Citation
"Normal Modes of a Double Pendulum"
http://demonstrations.wolfram.com/NormalModesOfADoublePendulum/
Wolfram Demonstrations Project
Published: March 7 2011