Numerical Solution of Some Fractional Diffusion Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
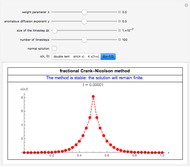
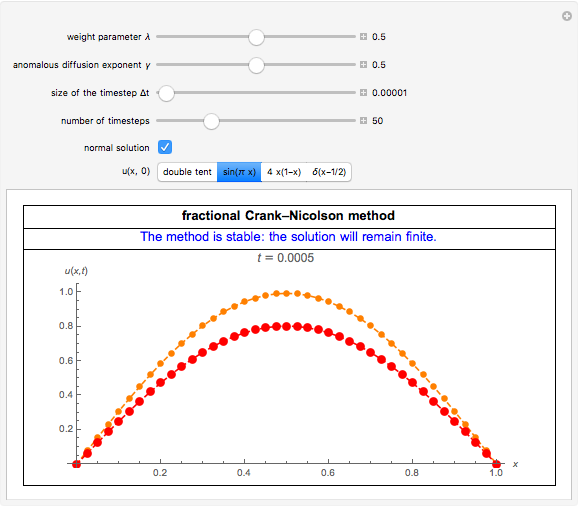
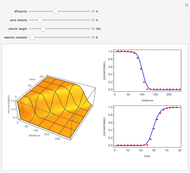
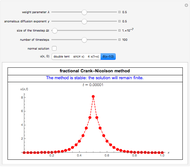
This Demonstration shows numerical solutions 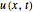 of the fractional diffusion equation by means of weighted average methods (or
of the fractional diffusion equation by means of weighted average methods (or  methods). The boundary conditions specify that the solution
methods). The boundary conditions specify that the solution  equals zero at
equals zero at  and
and 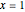 . Four different initial conditions can be chosen. When the weight parameter
. Four different initial conditions can be chosen. When the weight parameter 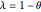 equals 1/2, the numerical method is the fractional Crank–Nicolson method. When the "normal solution" checkbox is checked, the normal diffusion solution is also plotted.
equals 1/2, the numerical method is the fractional Crank–Nicolson method. When the "normal solution" checkbox is checked, the normal diffusion solution is also plotted.
Contributed by: Santos Bravo Yuste (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The fractional diffusion equation is 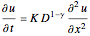 , where the
, where the 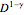 is the Riemann–Liouville derivative of order
is the Riemann–Liouville derivative of order  ,
, 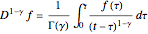 , is solved numerically by means of the fractional difference weighted-average methods (or
, is solved numerically by means of the fractional difference weighted-average methods (or  methods) discussed in [1]. When
methods) discussed in [1]. When  , the equation is just the normal diffusion equation and these methods become normal weighted-average methods [2]. Depending on the value of the weight factor
, the equation is just the normal diffusion equation and these methods become normal weighted-average methods [2]. Depending on the value of the weight factor 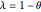 , the method can be fully implicit when
, the method can be fully implicit when  , or fully explicit when
, or fully explicit when 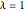 . The fractional Crank–Nicolson method for
. The fractional Crank–Nicolson method for 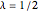 , or for other values of
, or for other values of 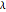 , is a generic
, is a generic 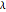 -weighted-average method. It is also determined whether the stability criterion of equation (35) of [1] is also satisfied. The size
-weighted-average method. It is also determined whether the stability criterion of equation (35) of [1] is also satisfied. The size 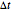 of the timestep and the number
of the timestep and the number  of timesteps can be chosen. The diffusion constant
of timesteps can be chosen. The diffusion constant 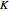 and the space discretization
and the space discretization 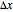 are fixed to 1 and
are fixed to 1 and 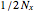 with
with  , respectively. When the "normal solution" checkbox is checked, the normal diffusion solution (
, respectively. When the "normal solution" checkbox is checked, the normal diffusion solution ( ) is also plotted (orange points). The broken lines are to guide the eye. The values of the numerical solutions are shown when the mouse pointer is over the points.
) is also plotted (orange points). The broken lines are to guide the eye. The values of the numerical solutions are shown when the mouse pointer is over the points.
References
[1] S. B. Yuste, "Weighted Average Finite Difference Methods for Fractional Diffusion Equations," Journal of Computational Physics, 216, 2006 pp. 264–274.
[2] K. W. Morton and D. F. Mayers, Numerical Solution of Partial Differential Equations, Cambridge: Cambridge University Press, 1994.
Permanent Citation