Details

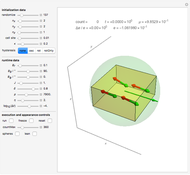
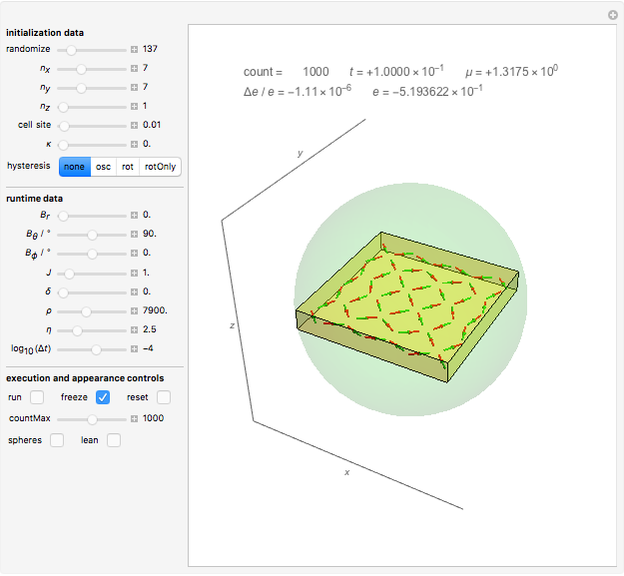
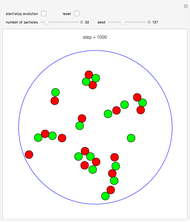
Snapshot 1: a 2D configuration resulting by decay from a well-aligned configuration of pure dipoles

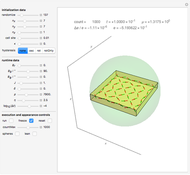
Snapshot 2: a 2D configuration resulting by decay from a random configuration of pairs of poles

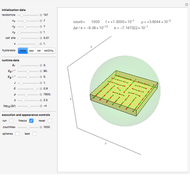
Snapshot 3: a 2D configuration resulting by decay from a not-so-well-aligned configuration of pairs of poles

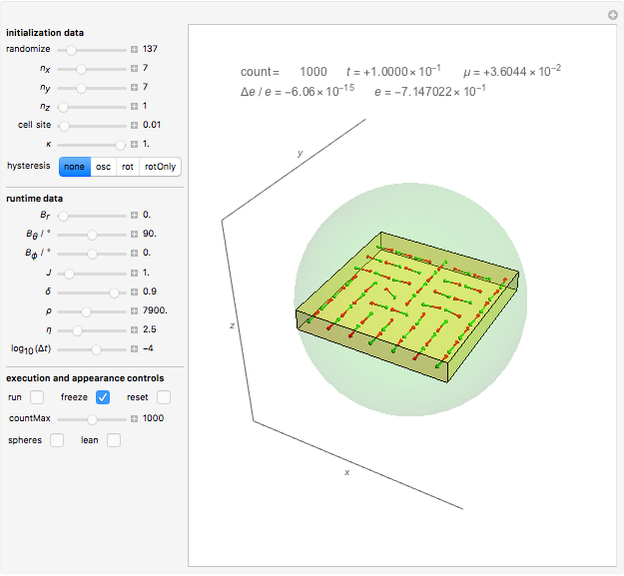
Snapshot 4: restoring alignment in the last phase of the hysteresis curve

Snapshot 5: restoring alignment in the last phase of the hysteresis curve, continued

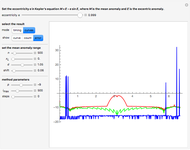
Snapshot 6: hysteresis curve for pairs of poles

Snapshot 7: hysteresis curve for pure dipoles

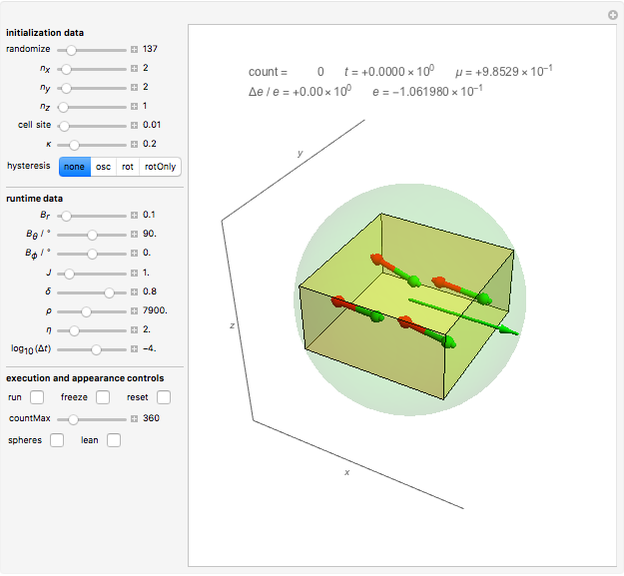
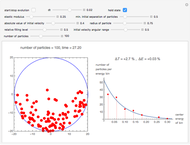
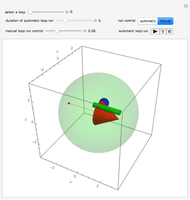
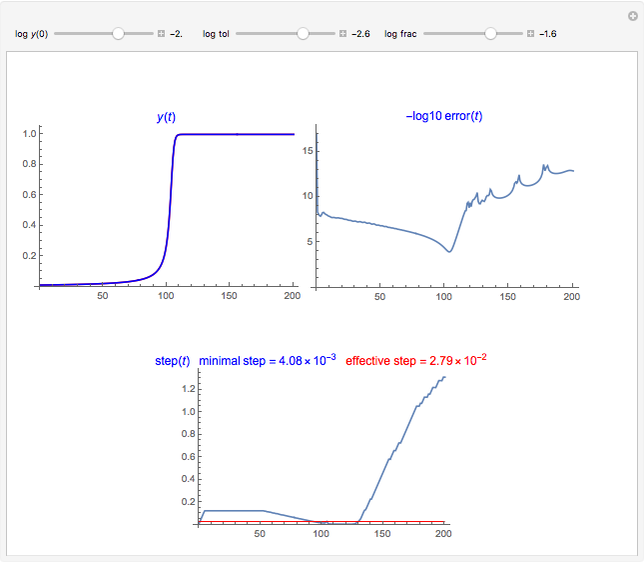
A finite part of a cubic lattice is shown, where each lattice point is the center of a freely rotatable, uniformly magnetized, spherical particle. Further, the particles are under the influence of a homogeneous magnetic field. The device that holds the particles in place (e.g. ball cages with diamond-coated contact surfaces) is assumed to cause negligible friction. However, friction is introduced by putting the particles into a bath of viscous liquid. This Demonstration gives numerical values (in SI units without a prefix) to all these quantities and follows the time evolution of the particles in a graphic that represents the direction of magnetic polarization as stylized compass needles.

So far, we have put forward a realistic physical constitution of the system under consideration. This system differs from Ewing's in an essential point: Whereas uniformly magnetized spheres behave exactly like true magnetic dipoles (see [3]), Ewing used magnetized pivoted steel bars. These can be a good approximation replaced by a pair of magnetic poles (in the limit of vanishing thickness, a uniformly magnetized straight piece of wire has exactly two magnetic poles at its ends). We take this into account by replacing the magnetic moment of the magnetized spheres by two magnetic poles of opposite sign. The strength of these poles is chosen such that the magnetic moment equals that of the spherical particle. The distance of the poles can be continuously moved between the two extremes: close to zero and the diameter of the spherical particle. The moment of inertia of the particle (also referred to as a needle) is taken as that of the spherical particle, independent of the positioning of the poles. (For meter-sized particles, a design would be a simple engineering task).

By changing the pole distance, we learn that the fate of well-aligned states strongly depends on it: For a small distance ( in our case), the parallel order always decays in the absence of an external magnetic field in a way that no needle can be found in the end that has nearly the same direction as all its direct lattice neighbors. For large distances (e.g. ), even loosely aligned configurations develop in the absence of an external magnetic field into a well-aligned stable configuration. Since Ewing's observations exclusively are on this second case, his observations of stable, ordered domains agree with the present computational model.

Ewing may not have been aware of the detailed nature of the bar magnet for this observation. In considering the observation as an explanation of ferromagnetism, one had to stipulate tiny bar magnets (i.e. pairs of poles) in the iron atoms and not magnetic dipoles. As we know today, quantum mechanical exchange interaction is needed to allow for large, stable, uniformly aligned magnetic domains, such as Weiss's domains in iron. Also the quantum mechanical case can be meaningfully treated as a Demonstration [4].

Apart from the specific law of force, the dynamical algorithm for the particles is the same as in [2]. It makes use of Euler–Rodrigues parameters [5, 6] as dynamical variables and a Verlet integrator for stepwise evolution.

References

[1] J. A. Ewing, Magnetic Induction in Iron and Other Metals (3rd ed.), New York: The D. Van Nostrand Company, 1900. (Jun 26, 2019) archive.org/details/magneticinductio00ewinrich.

[2] U. Mutze. "On the Ewing Model of Magnetism" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/OnTheEwingModelOfMagnetism.

[3] B. F. Edwards, D. M. Riffe, J.-Y. Ji and W. A. Booth, "Interactions between Uniformly Magnetized Spheres," American Journal of Physics, 85(130), 2017. doi:10.1119/1.4973409.

[4] U. Mutze. "Dynamics of Qubit Lattices" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/DynamicsOfQubitLattices.

[5] U. Mutze, "Rigidly Connected Overlapping Spherical Particles: A Versatile Grain Model," Granular Matter, 8(3–4), 2006 pp. 185–194. doi:10.1007/s10035-006-0011-5.

[6] U. Mutze. "Polyspherical Grains and Their Dynamics." (Jun 26, 2019) www.ulrichmutze.de/articles/07-252.pdf.