One-Dimensional Fractional Brownian Motion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
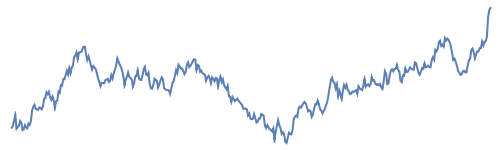
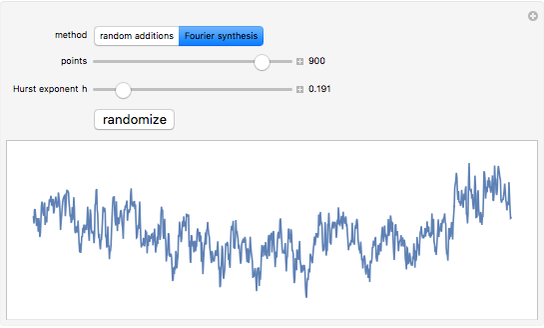
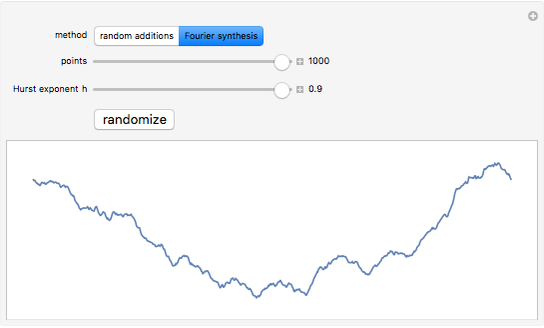
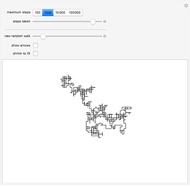
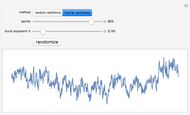
Two methods for generating a fractional Brownian motion to simulate a natural surface are demonstrated here. The Hurst exponent  describes the raggedness, with higher exponents leading to smoother surfaces. Fractional Brownian motion is a generalization of ordinary Brownian motion that has been used successfully to model a variety of natural phenomena, such as terrains, coastlines, and clouds. It has the scaling property
describes the raggedness, with higher exponents leading to smoother surfaces. Fractional Brownian motion is a generalization of ordinary Brownian motion that has been used successfully to model a variety of natural phenomena, such as terrains, coastlines, and clouds. It has the scaling property  . Ordinary Brownian motion has
. Ordinary Brownian motion has  .
.
Contributed by: Roman E. Maeder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
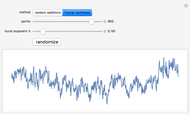
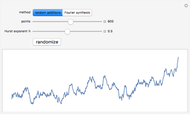
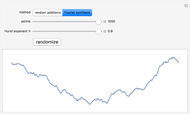
Random addition refines the list of points by interpolation and adding random offsets.
Fourier synthesis generates a random spectrum such that the resulting data has the correct scaling property.
The code for generating the data is from Roman E. Maeder, The Mathematica Programmer II, New York: Academic Press, 1996.
Permanent Citation
"One-Dimensional Fractional Brownian Motion"
http://demonstrations.wolfram.com/OneDimensionalFractionalBrownianMotion/
Wolfram Demonstrations Project
Published: March 7 2011