Optical Filter with Sinusoidally Varying Permittivity Using Mathieu's Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
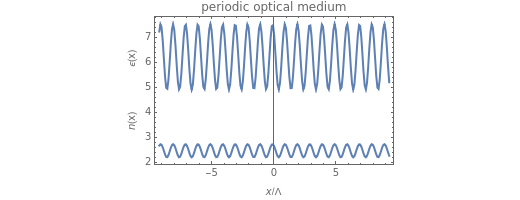
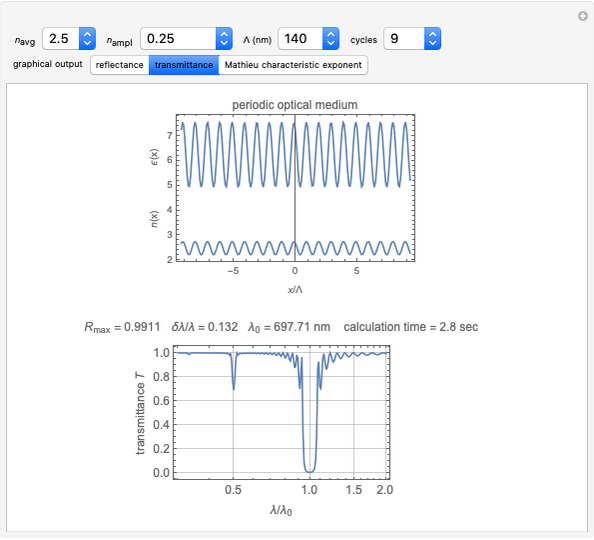
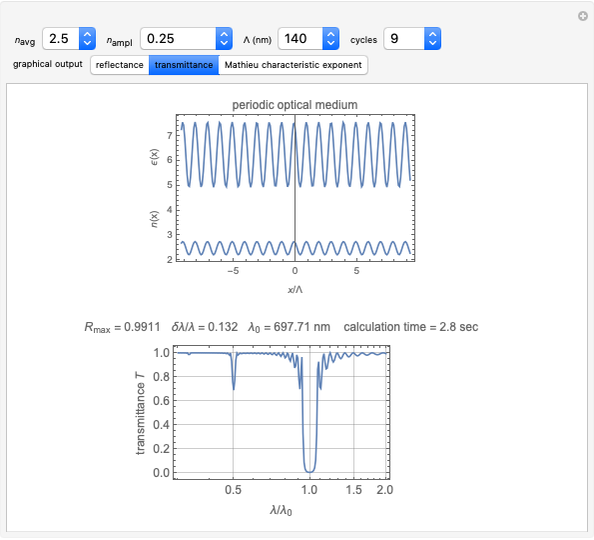
This Demonstration shows the reflection and transmission of light propagating through a dielectric whose permittivity  varies sinusoidally in the direction of propagation. Reflectance and transmittance can be displayed as a function of the number of periods of the truncated permittivity sinusoid. The effect of the sinusoid amplitude is displayed along with reflectance/transmittance. The reflectance, the wavelength at maximum reflectance
varies sinusoidally in the direction of propagation. Reflectance and transmittance can be displayed as a function of the number of periods of the truncated permittivity sinusoid. The effect of the sinusoid amplitude is displayed along with reflectance/transmittance. The reflectance, the wavelength at maximum reflectance 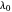 and the width of the peak
and the width of the peak 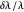 are displayed within the graphic. Forbidden optical ranges occur in the imaginary part of the characteristic equation.
are displayed within the graphic. Forbidden optical ranges occur in the imaginary part of the characteristic equation.
Contributed by: Rodolfo Quintero (July 2020)
(CINVESTAV, Mexico)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Propagation of waves through sinusoidally varying permittivity media [4]
A plane electromagnetic wave with an electric field 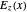 , propagating through an isotropic and uniform medium, obeys the equation
, propagating through an isotropic and uniform medium, obeys the equation
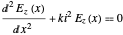 , where
, where 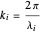 , (1)
, (1)
and has a general solution composed of forward- and backward-propagating plane waves
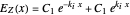 . (2)
. (2)
This wave impinges on a rugate filter with a sinusoidally varying permittivity 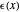 ,
,
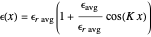 ,
, 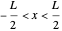 . (3)
. (3)
This results in Mathieu's differential equation [1],
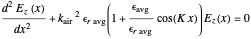 , (4)
, (4)
whose analytic solution is a linear combination of Mathieu 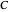 functions [2]
functions [2]
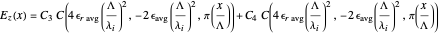 . (5)
. (5)
The equation in the emerging side is also (1), but with different integration constants
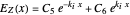 . (6)
. (6)
Boundary conditions [4]
If the output medium is semi-infinite to the right, there is no reflected wave, therefore 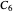 is equal to zero.
is equal to zero.
From Maxwell equations, it can be shown that 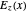 and
and  have to be continuous at the input and output boundaries. The integration constants
have to be continuous at the input and output boundaries. The integration constants 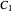 to
to 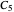 are calculated from these conditions.
are calculated from these conditions.
The reflected power 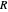 is thus defined as
is thus defined as
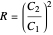 . (7)
. (7)
Such a filter reflects the forward-propagating wave strongly at Bragg wavelengths ( for
for 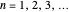 ), due to interference of incoming and reflected waves, creating reflection peaks.
), due to interference of incoming and reflected waves, creating reflection peaks.
Eigenvalues
If (4) is written as
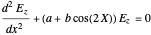 , (8)
, (8)
where
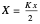 ,
, 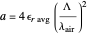 ,
,
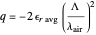
and the period in 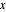 is
is 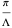 .
.
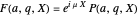 ,
,
where  are the eigenvalues, and
are the eigenvalues, and 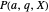 has period
has period 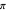 :
:
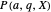 and
and 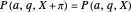 .
.
The eigenvalues  can be calculated with the following Wolfram Language function:
can be calculated with the following Wolfram Language function:
 MathieuCharacteristicExponent[a, b]. (9)
MathieuCharacteristicExponent[a, b]. (9)
Reflection takes place in the  ranges where
ranges where  is complex, and transmission where
is complex, and transmission where  is real. The forbidden or reflection bands calculated with (9) are the same as those calculated with (7).
is real. The forbidden or reflection bands calculated with (9) are the same as those calculated with (7).
Controls
 , defined by
, defined by 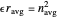 , is the permittivity of the filter base material as well as the permittivity of the input and output sections.
, is the permittivity of the filter base material as well as the permittivity of the input and output sections.
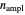 defines, together with
defines, together with 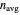 , the amplitude
, the amplitude 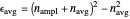 of the sinusoidal function of the filter.
of the sinusoidal function of the filter.
 (nm) is the period of
(nm) is the period of 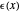 , that is,
, that is, 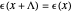 ;
; 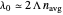 is the wavelength of reflectance peak, according to a quarter wavelength Bragg reflection approximation.
is the wavelength of reflectance peak, according to a quarter wavelength Bragg reflection approximation.
cycles is the number of complete cycles of the sinusoid. Reflectance 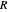 increases with the number of cycles.
increases with the number of cycles.
graphical output:
"reflectance" is reflectance of the filter.  increases with cycles and
increases with cycles and  .
.
"transmittance" is transmittance of the filter, 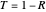 .
.
"Mathieu characteristic exponent": identifies the forbidden transmission bands, or equivalently the reflective bands. They do not depend on boundary conditions.
Snapshot captions
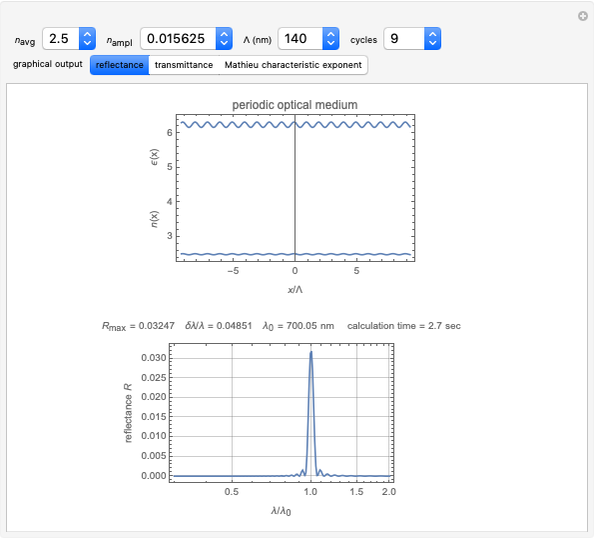
Snapshot 1: if  , contrast is low, as is reflectance
, contrast is low, as is reflectance
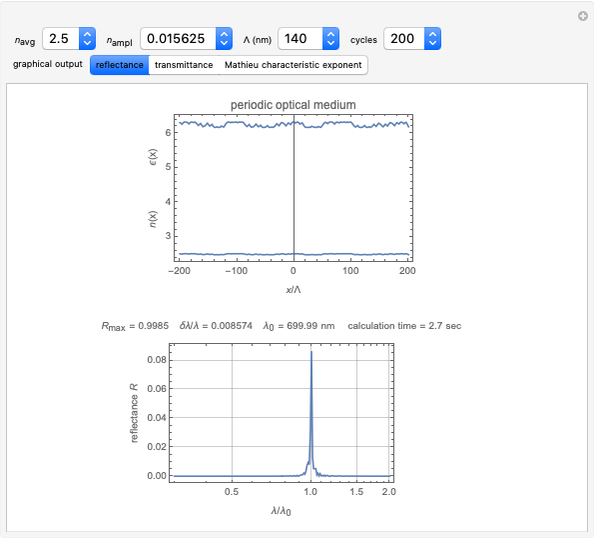
Snapshot 2: if 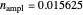 as before, but the number of cycles is increased to 200, reflectivity increases to
as before, but the number of cycles is increased to 200, reflectivity increases to 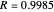
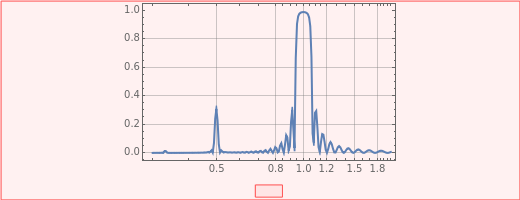
Snapshot 3: Reflecting peaks occur at 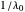 ,
, 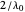 ,
,  , … with decreasing amplitude. Only the first two peaks are shown; they do not depend on specific boundary conditions.
, … with decreasing amplitude. Only the first two peaks are shown; they do not depend on specific boundary conditions.
References
[1] E. W. Weisstein, "Mathieu Differential Equation" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/MathieuDifferentialEquation.html (Wolfram MathWorld).
[2] E. W. Weisstein, "Mathieu Function" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/MathieuFunction.html (Wolfram MathWorld).
[3] Wikipedia. "Mathieu Function." (Jan 8, 2020) en.wikipedia.org/wiki/Mathieu_function.
[4] P. Yeh, Optical Waves in Layered Media, New York: John Wiley, 1988.
Permanent Citation