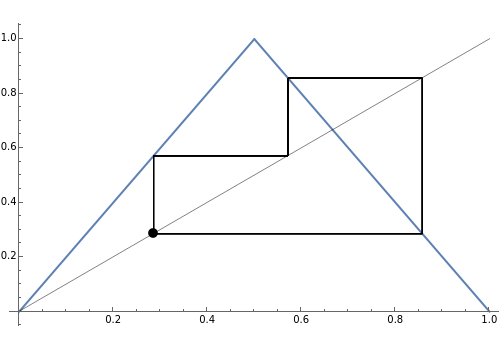
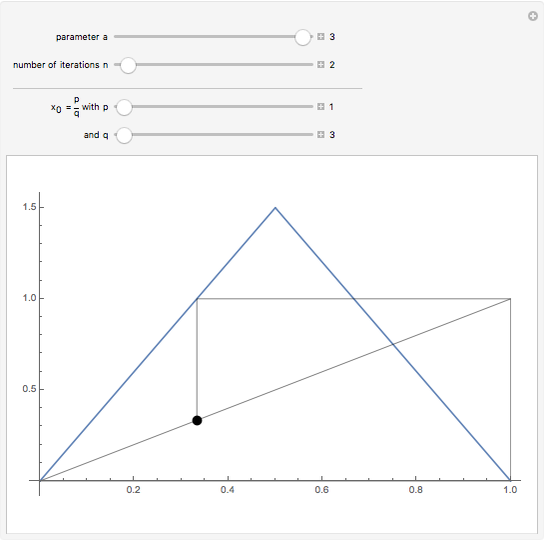
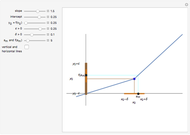
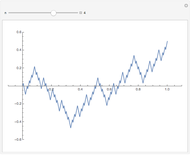
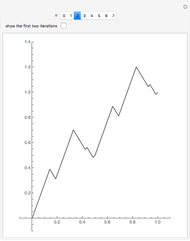
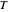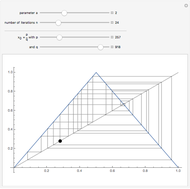
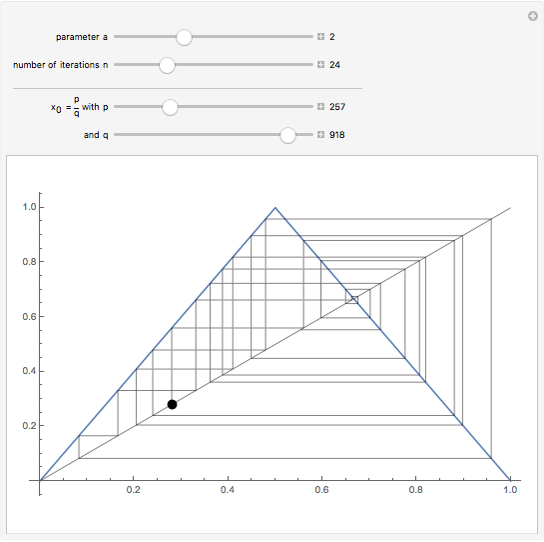
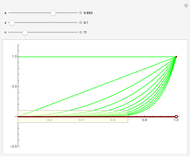
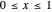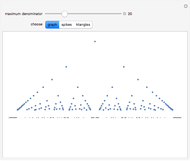
The iterates xn+1=Ta(xn), where is the slope of the tent function , describe orbits. All the interesting orbits lie within the unit interval . That T shows orbits of period three implies that T is chaotic on the unit interval. Many of the orbits of T3 leave the unit interval and have orbits that tend to 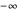. You can see that any middle-third interval, constructed exactly as in the Cantor set, leaves the unit interval. Conversely, you can see that it is precisely the points of the Cantor set that have orbits that do not tend to 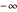. Thus all the interesting dynamics for T3 take place on a fractal, the Cantor set.