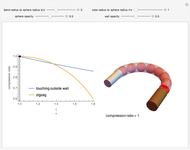
Packing Spheres into a Thin Cylinder

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The densest packing of spheres with radius  in a cylinder of radius
in a cylinder of radius  , where
, where  , is a challenging problem. This Demonstration provides the optimal packing for small ratios of
, is a challenging problem. This Demonstration provides the optimal packing for small ratios of  and upper bounds that show dense packings up to
and upper bounds that show dense packings up to  .
.
Contributed by: Aaron T. Becker and Li Huang (May 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
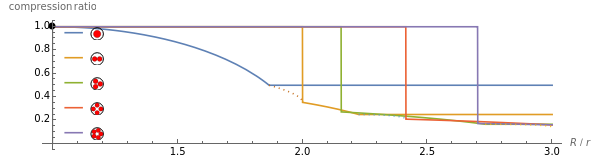
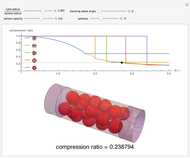
When  , the spheres are packed in a straight line. The polygonal line joining the centers zigzags as the tube radius
, the spheres are packed in a straight line. The polygonal line joining the centers zigzags as the tube radius  increases until
increases until  , at which point the spheres are stacked in two columns. As
, at which point the spheres are stacked in two columns. As  increases, these columns twist into a helix until
increases, these columns twist into a helix until  . Next, the spheres are arranged in parallel sets of two, each set oriented 90° from the previous. These compress, briefly shift to a more dense packing of sets of three, then revert to sets of two until they form four columns of spheres. These columns twist, then switch back to sets of three, briefly interrupted by arrangements of sets of five, and then the sets of three twist until they end forming sets of hexagons at
. Next, the spheres are arranged in parallel sets of two, each set oriented 90° from the previous. These compress, briefly shift to a more dense packing of sets of three, then revert to sets of two until they form four columns of spheres. These columns twist, then switch back to sets of three, briefly interrupted by arrangements of sets of five, and then the sets of three twist until they end forming sets of hexagons at  .
.
For analytical results derived from numerical optimization up to  , see [1], which identified 40 densest arrangements in this range. This Demonstration only shows eight of these structures, which are thus upper bounds for the minimum density.
, see [1], which identified 40 densest arrangements in this range. This Demonstration only shows eight of these structures, which are thus upper bounds for the minimum density.
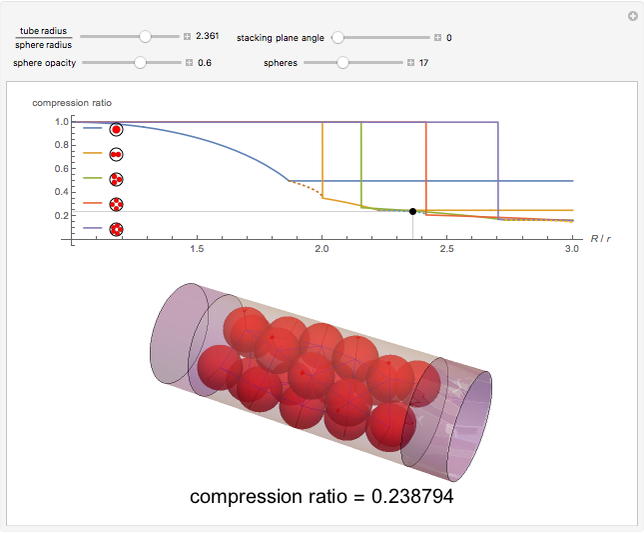
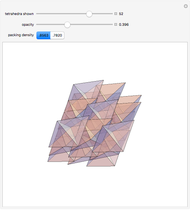
Varying the opacity of the spheres lets you see the sphere-sphere contacts and sphere-cylinder contacts. Sphere-sphere contacts are drawn in blue, and sphere-cylinder contacts in black. This Demonstration only includes structures where each sphere is in contact with the cylinder, so that there are no internal spheres. Structures above  include internal spheres, while those below do not.
include internal spheres, while those below do not.
The structure forms regular crystalline structures that are highlighted in the plot and have alternating repeating layers. These layers are:
two at a time at  ,
,
three at a time at  ,
,
four at a time at  ,
,
five at a time at  ,
,
six at a time at  .
.
Reference
[1] A. Mughal, H. K. Chan, D. Weaire, and S. Hutzler, "Dense Packings of Spheres in Cylinders I: Simulations." arxiv.org/abs/1203.3373.
Permanent Citation