Pandiagonal Magic Squares of Order Five

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
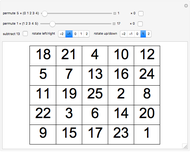
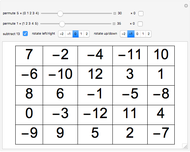
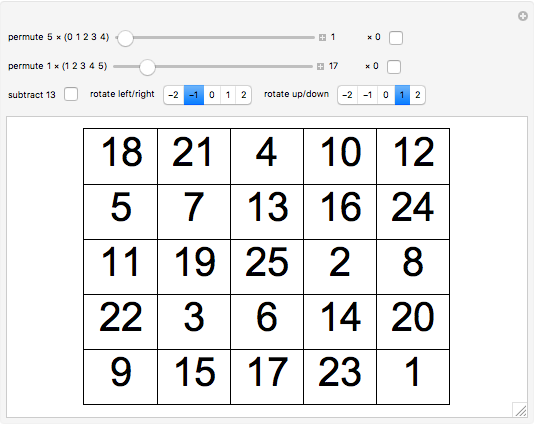
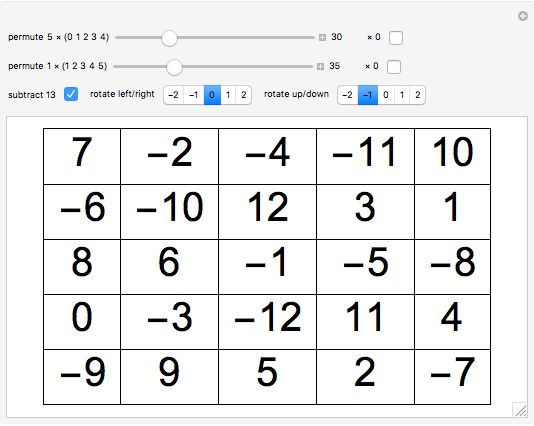
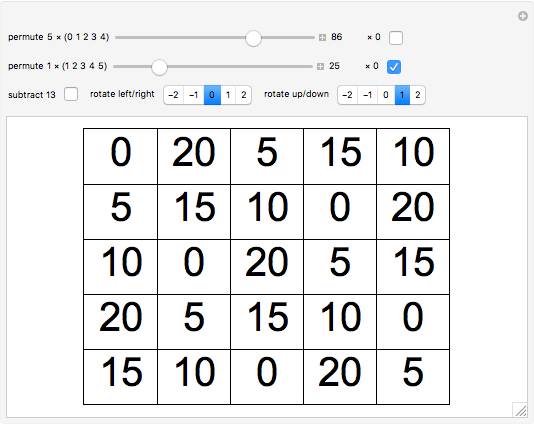
A magic square has the same sums for the numbers in the rows, columns, and main diagonals. In a pandiagonal magic square, the square can be rotated as if the edges were wrapped around (like a rubber square sheet can be made into a torus), and the main diagonals will still add up to the same magic sum (65 here). All of the 5×5 pandiagonal magic squares can be generated by adding together two sets of permutations.
Contributed by: Ed Pegg Jr (February 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
By one count, there are 3600 order-5 pandiagonal magic squares [1]. If you would like to generate all 275,305,224 order-5 magic squares, try [2].
Reference
[1] H. Heinz. "Pandiagonal 5×5." (Feb 17, 2016) recmath.org/Magic%20 Squares/pandiag5.htm.
[2] Netstaff Co., Inc. "Magic Squares." (Feb 17, 2016) www.netstaff.co.jp/msq/msqe.htm.
Permanent Citation
"Pandiagonal Magic Squares of Order Five"
http://demonstrations.wolfram.com/PandiagonalMagicSquaresOfOrderFive/
Wolfram Demonstrations Project
Published: February 18 2016