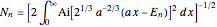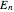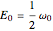Particle in an Infinite Vee Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
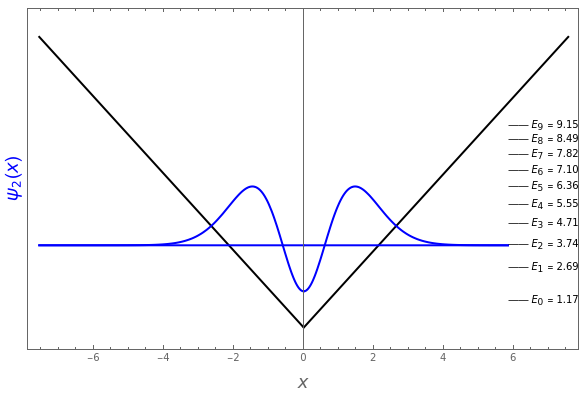
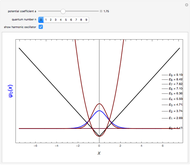
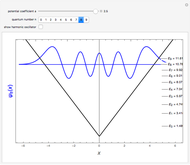
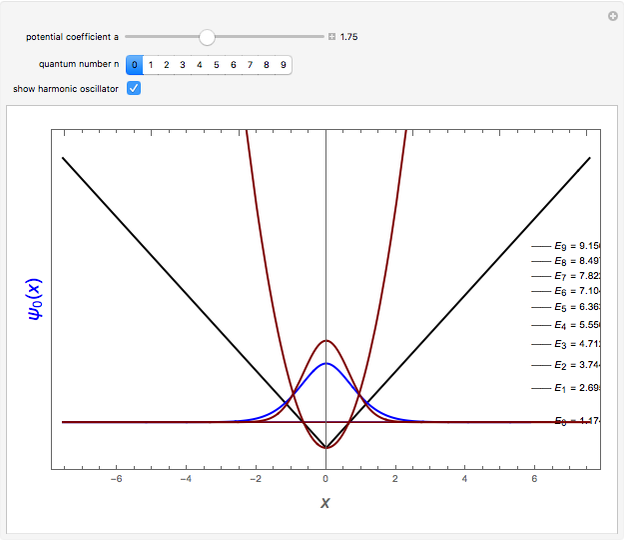
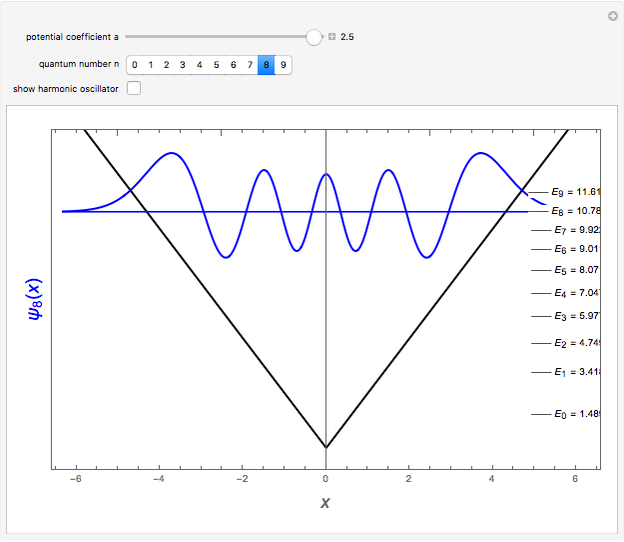
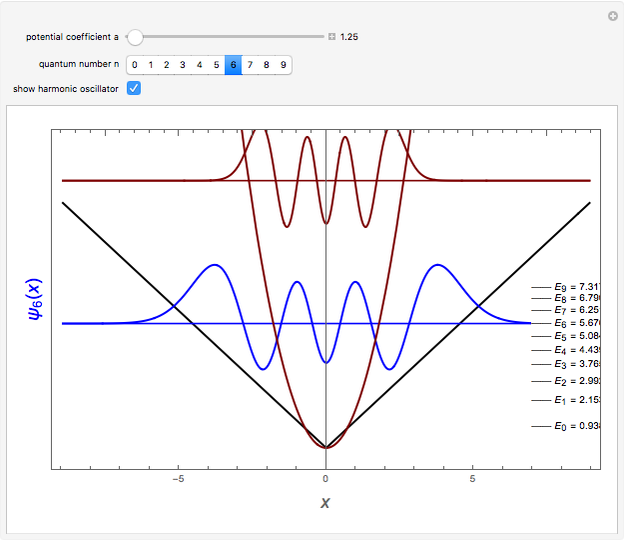
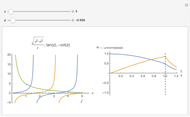
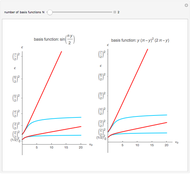
This Demonstration considers solutions of the Schrödinger equation for a particle in a one-dimensional "infinite vee" potential: 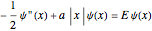 , setting
, setting 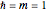 for simplicity. The solutions of the differential equation that approach zero as
for simplicity. The solutions of the differential equation that approach zero as 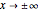 are Airy functions
are Airy functions 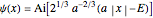 , as can be found using DSolve in Mathematica. The allowed values of
, as can be found using DSolve in Mathematica. The allowed values of  are found by requiring continuity of
are found by requiring continuity of 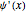 at
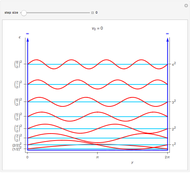
at  . The even solutions
. The even solutions 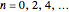 require
require  , which leads to
, which leads to 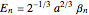 , with
, with 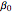 ,
, 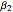 ,
, 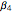 , … being the first, second, third, … zeros of the Airy prime function:
, … being the first, second, third, … zeros of the Airy prime function: 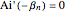 . The odd solutions
. The odd solutions 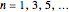 have nodes
have nodes 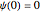 , which leads to
, which leads to 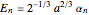 , with
, with 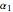 ,
,  ,
, 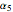 , … being the first, second, third, … zeros of the Airy function:
, … being the first, second, third, … zeros of the Airy function:  . The ground state is given by
. The ground state is given by 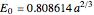 .
.
Contributed by: S. M. Blinder (November 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation