Peculiar Behavior of the Newton Method
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
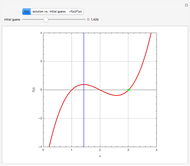
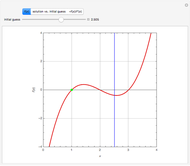
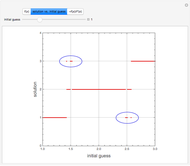
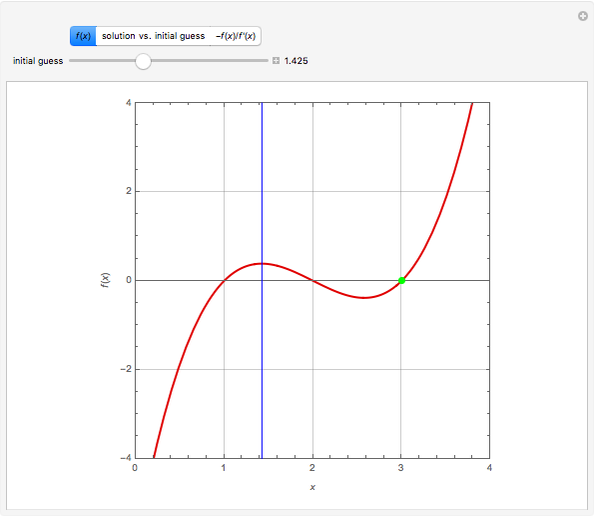
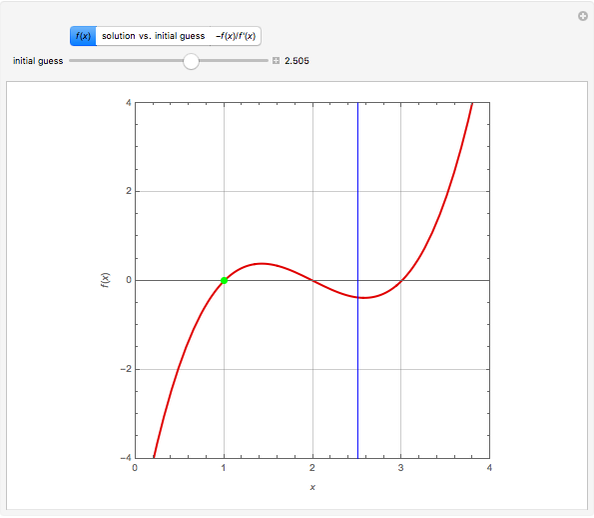
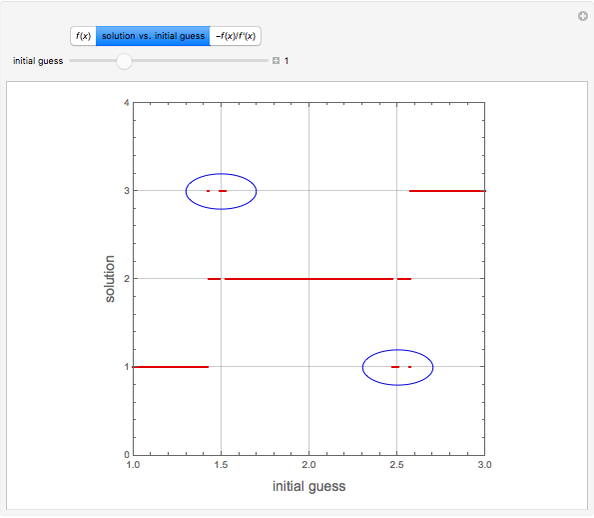
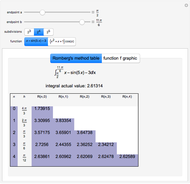
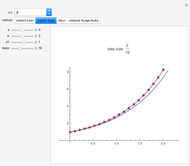
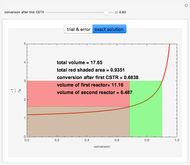
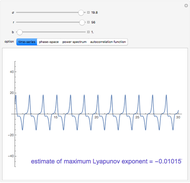
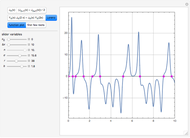
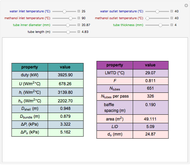
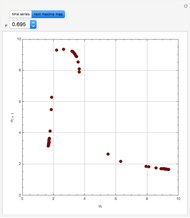
Consider the function  , which has the three obvious roots 1, 2, and 3. These roots can be obtained using the Newton technique
, which has the three obvious roots 1, 2, and 3. These roots can be obtained using the Newton technique
Contributed by: Housam Binous (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] K. J. Beers, Numerical Methods for Chemical Engineering, Cambridge: Cambridge University Press, 2007.
Permanent Citation