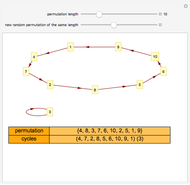
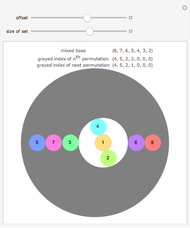
The number of ways to arrange  different objects in a row is
different objects in a row is  . The exclamation mark "!" is read as "factorial". Of course, the product is the same in reverse order:
. The exclamation mark "!" is read as "factorial". Of course, the product is the same in reverse order:  . Each such arrangement is called a permutation. For consistency, it is assumed that
. Each such arrangement is called a permutation. For consistency, it is assumed that  .
.
Number of k-Permutations
If only  of the
of the  objects are to be arranged in a row, the formula is
objects are to be arranged in a row, the formula is
 ,
,
with  factors. If
factors. If  ,
,  . Such an arrangement is called a partial permutation, or a
. Such an arrangement is called a partial permutation, or a  -permutation. Clearly
-permutation. Clearly  , because all
, because all  objects are being arranged; the formula reduces to
objects are being arranged; the formula reduces to  because the denominator is
because the denominator is  .
.
Number of Combinations
The number of ways to choose a subset of  objects from
objects from  objects is
objects is
 .
.
Therefore,  . Each choice of a subset is called a combination. Another notation for
. Each choice of a subset is called a combination. Another notation for  is
is  . Again, if
. Again, if  ,
,  . A special case is
. A special case is  .
.
[less]