Phonon Modes for 2D Lattice Vibrations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
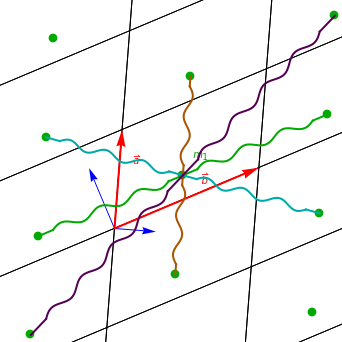
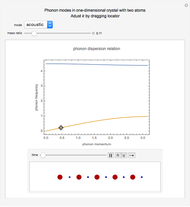
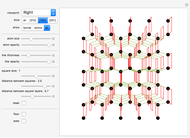
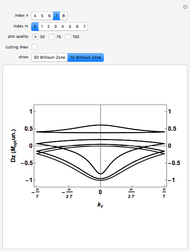
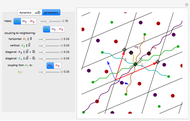
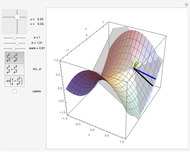
A lattice of atoms can be modeled as harmonic oscillators, with forces proportional to the displacements of the atoms from equilibrium positions. The simplest such model introduces coupling only between nearest-neighbor atoms. In this Demonstration, a lattice cell containing one to five atoms is modeled, with nearest-neighbor harmonic coupling to the masses in each nearby cell. Normal mode solutions to these equations of motion are plotted. Controls are provided to alter the coupling "spring constants" and other free parameters, as well as controls to select from the reciprocal space vectors and angular frequencies associated with the normal mode solutions. A time control is also provided to display changes of the lattice through one period of the lattice vibration. A plot of the dispersion relation, showing the angular velocities associated with each reciprocal vector, is also provided.
Contributed by: Peeter Joot (April 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The positions of masses within a two-dimensional periodic array of cells can be described by summing the lattice vector 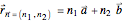 , representing the origin of each of the lattice cells, and a relative vector to the position of each of the masses. With
, representing the origin of each of the lattice cells, and a relative vector to the position of each of the masses. With 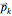 representing the equilibrium position of the
representing the equilibrium position of the 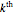 mass in cell
mass in cell 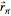 , the position of that mass is
, the position of that mass is 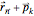 .
.
Let  , with direction
, with direction 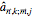 , represent the equilibrium separation of the
, represent the equilibrium separation of the 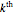 mass in cell
mass in cell 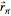 from the
from the  mass in cell
mass in cell  . If the harmonic coupling between these masses has magnitude
. If the harmonic coupling between these masses has magnitude 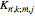 , then the system of equations describing the vector displacement
, then the system of equations describing the vector displacement 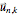 for the
for the 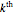 mass in unit cell
mass in unit cell  from the equilibrium position is given by
from the equilibrium position is given by
 .
.
In general, we have one such equation for each 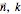 pair. A trial solution of the form:
pair. A trial solution of the form: 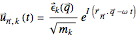 can be used to decouple this system, resulting in a single equation for each
can be used to decouple this system, resulting in a single equation for each 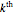 mass of the form
mass of the form
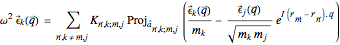 .
.
This describes all the steady-state lattice vibrations, the normal modes, that can be modeled by this trial solution. Here  is a vector in reciprocal space, effectively parameterizing the angular velocity
is a vector in reciprocal space, effectively parameterizing the angular velocity 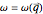 . The vector
. The vector 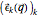 is an eigenvector of the equations of motion of the system for this assumed solution, where
is an eigenvector of the equations of motion of the system for this assumed solution, where 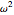 are the eigenvalues of this system. For an
are the eigenvalues of this system. For an  -atom basis, there are
-atom basis, there are  such
such 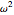 eigenvalues per
eigenvalues per  point, each resulting in a different characteristic motion.
point, each resulting in a different characteristic motion.
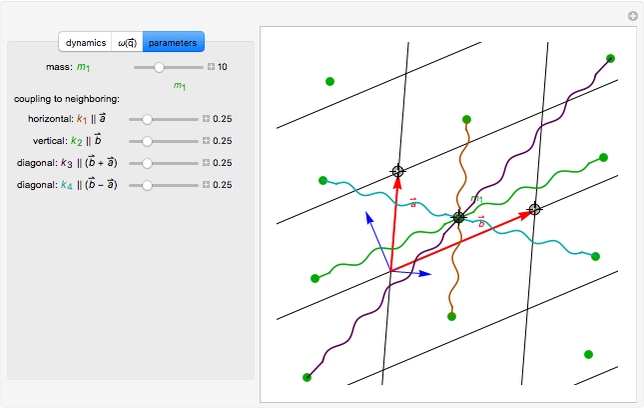
The rank of the resulting eigenvalue problem depends on the number of masses per unit cell, but the complexity of the matrix expression depends on the number of neighboring interactions that are considered. For example, given lattice vectors 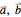 , diagonals
, diagonals 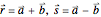 , and a one-atom basis, where each unit cell contains a single mass coupled with harmonic oscillator forces between only nearest neighbors, the normal mode solutions follow from the solution of the eigenvalue problem
, and a one-atom basis, where each unit cell contains a single mass coupled with harmonic oscillator forces between only nearest neighbors, the normal mode solutions follow from the solution of the eigenvalue problem
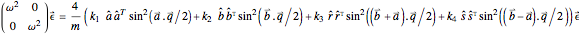 .
.
Controls are provided to display the dynamics associated with each of the characteristic angular frequencies  , for given reciprocal vector values
, for given reciprocal vector values  .
.
Three tabs are provided in this Demonstration. The primary tab displays the dynamics of the solution for particular pair of  values. In that tab, selecting "Play" for the time control animates the lattice vibrations. A scaling control is provided to alter the initial magnitude of the eigenvectors, tantamount to picking the initial time boundary value constraints. Note that it is possible to select physically unrealistic scaling factors that allow for collisions that are not modeled by this system.
values. In that tab, selecting "Play" for the time control animates the lattice vibrations. A scaling control is provided to alter the initial magnitude of the eigenvectors, tantamount to picking the initial time boundary value constraints. Note that it is possible to select physically unrealistic scaling factors that allow for collisions that are not modeled by this system.
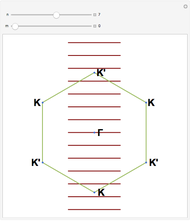
A second tab provides the dispersion relation, the dependence of angular velocity 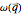 on all
on all  points.
points.
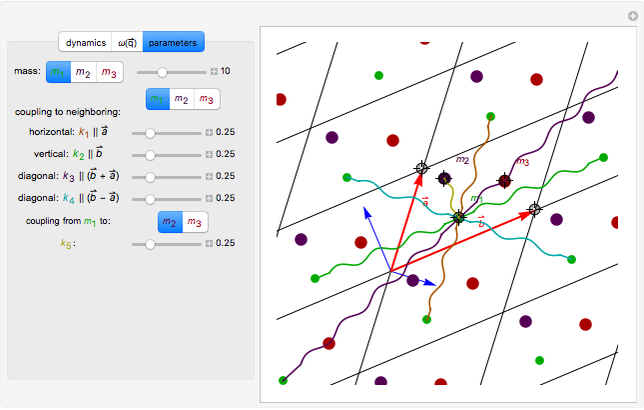
Finally, a parameters tab provides controls for the spring constants 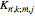 , the primitive unit cell lattice vectors
, the primitive unit cell lattice vectors 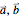 , and the positions of the masses
, and the positions of the masses 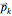 within each unit cell of the lattice. Additional mass position locators, up to five total, may be added or deleted by Alt-clicking the lattice cell in the desired location. For mass locator removal, it is necessary to adjust one of the other locators so that the removal takes effect. Note that it is possible to select equilibrium mass positions that are too close, leading to physically unrealistic dynamics, such as masses passing through each other.
within each unit cell of the lattice. Additional mass position locators, up to five total, may be added or deleted by Alt-clicking the lattice cell in the desired location. For mass locator removal, it is necessary to adjust one of the other locators so that the removal takes effect. Note that it is possible to select equilibrium mass positions that are too close, leading to physically unrealistic dynamics, such as masses passing through each other.
The total number of interactions, even when those interactions are restricted to just the neighboring lattice cells, increases quickly as additional masses per cell are added. For example, with three masses per unit cell, considering only the neighboring and origin cells, there are 29 interactions possible for each mass. To simplify the physical constants dialog, distinct "spring constant" selection is only available for a subset of the possible interactions. This imposes the following respective constraints along the "horizontal," "vertical," "NE diagonal," and "NW diagonal" directions connecting the masses across the cells
 ,
, 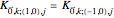 ,
, 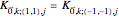 ,
, 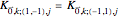 .
.
These are labeled  ,
, 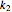 ,
, 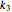 , and
, and 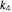 in the parameters tab, respectively. For example, the first identity above is the imposition of an equality constraint on the coupling constants in the "left" and "right" directions separating masses in neighboring "horizontal" cells (when the lattice is square). Those are the interactions directed primarily along the lattice vector directions
in the parameters tab, respectively. For example, the first identity above is the imposition of an equality constraint on the coupling constants in the "left" and "right" directions separating masses in neighboring "horizontal" cells (when the lattice is square). Those are the interactions directed primarily along the lattice vector directions 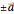 (primarily since these directions are also adjusted for the positions of the masses within the respective cells if different). Similarly, the same coupling constants are used for each of the pairs of directions that are directed primarily along the
(primarily since these directions are also adjusted for the positions of the masses within the respective cells if different). Similarly, the same coupling constants are used for each of the pairs of directions that are directed primarily along the 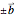 , ±(
, ±(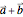 ), ±(
), ±(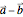 ) directions separating the lattice cells.
) directions separating the lattice cells.
When there is more than one mass per unit cell, distinct coupling constants for the intra-cell interactions between the masses within the origin unit cell may be selected (i.e. 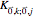 ). These are labeled
). These are labeled 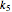 in the parameters tab.
in the parameters tab.
General theory describing oscillations around lattice equilibrium points can be found in [1].
Reference
[1] N. W. Ashcroft and N. D. Mermin, Solid State Physics, New York: Holt, Rinehart and Winston, 1976, Chapters 21 and 22.
Permanent Citation