Polyhedra with Prismatic Symmetry

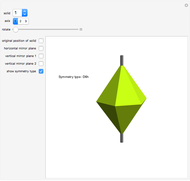
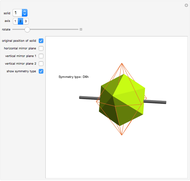
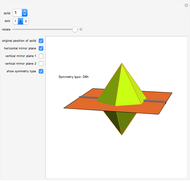
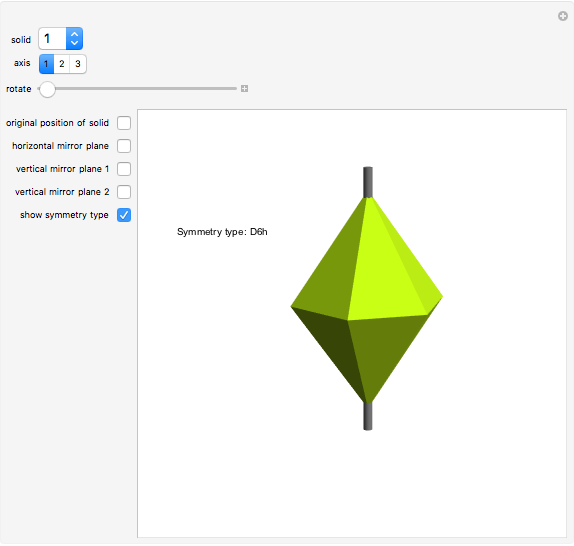
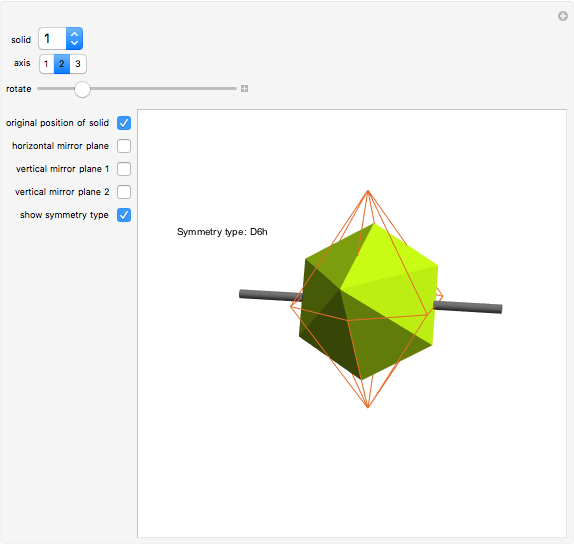
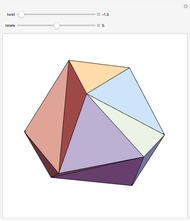
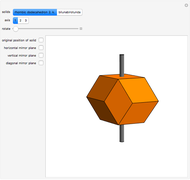
Polyhedra with cyclic (C) or dihedral (D) rotational symmetry are said to have prismatic symmetry type. A hexagonal-based prism has a principal axis of six-fold rotational symmetry (assume that the axis is vertical) and six secondary axes of two-fold symmetry (all are in the horizontal plane). There is a horizontal mirror plane (and there are vertical mirror planes as well). This system is labeled D6h. The hexagonal dipyramid has this symmetry type. If the horizontal mirror plane is destroyed, the system of type D6v is obtained. If all mirror planes are destroyed, the system is labeled D6.

A hexagonal-based pyramid has a six-fold axis of rotational symmetry (assume it is placed vertically). There are six vertical mirror planes. The system is labeled C6v. If all vertical mirror planes are destroyed, the system of type C6 is obtained. Assume a pyramid with symmetry type C6 is put on a plane and is reflected in the plane. The resulting dipyramid has a horizontal mirror symmetry. This type is labeled C6h.

P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1997 p. 302.