Potential and Current Distributions over a Disk Electrode with Vibrating Probe

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
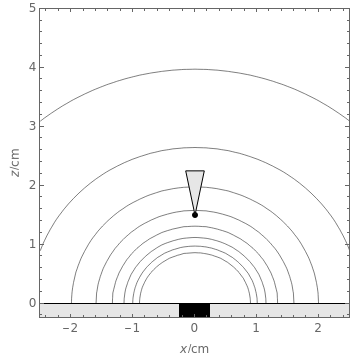
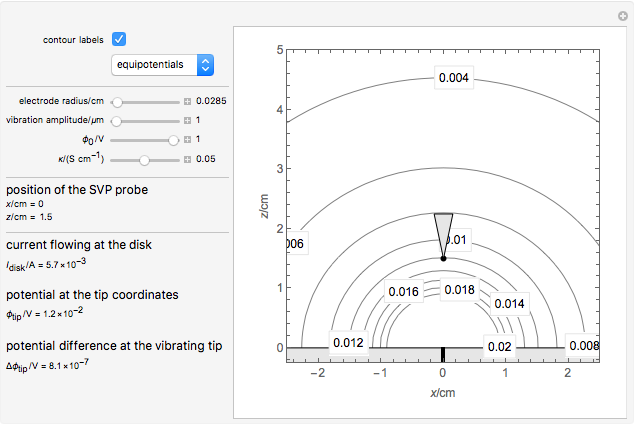
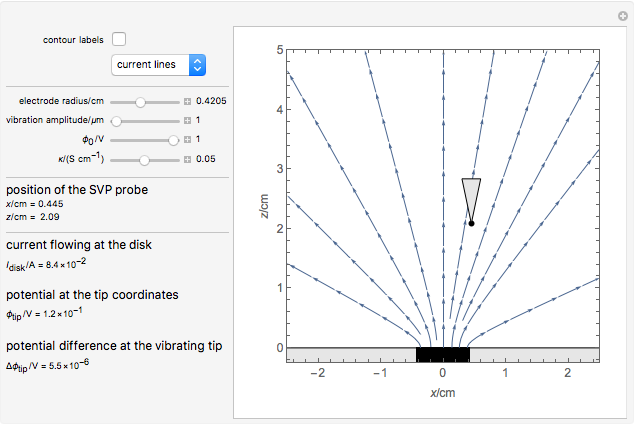
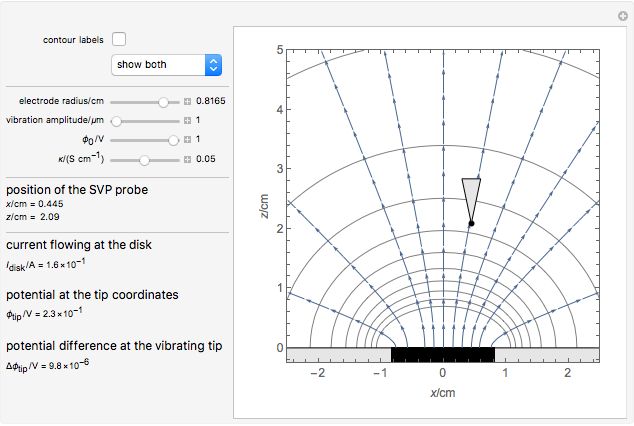
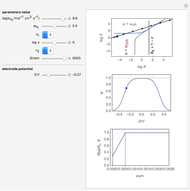
This Demonstration shows the primary current distribution over a disk electrode immersed in an electrolyte of constant conductivity and polarized at a constant voltage. The current distribution can be shown as current lines or as equipotential contours. In addition, the potential difference measured by a vibrating probe located in the solution is also determined. You can drag the probe, at position ( ,
,  ), and vary the amplitude of the vibration. The effect of the solution conductivity on the signal measured by the probe can also be demonstrated. Conductivities of 0.001 S/cm and 0.1 S/cm correspond roughly to solutions of 10 mM NaCl and 1 M NaCl, respectively.
), and vary the amplitude of the vibration. The effect of the solution conductivity on the signal measured by the probe can also be demonstrated. Conductivities of 0.001 S/cm and 0.1 S/cm correspond roughly to solutions of 10 mM NaCl and 1 M NaCl, respectively.
Contributed by: Nicolas Murer and Jean-Paul Diard (April 2016)
Bio-Logic SAS
Open content licensed under CC BY-NC-SA
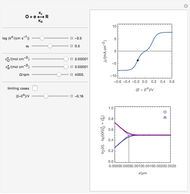
Snapshots
Details
The SVET (Scanning Vibrating Electrode Technique) is based on the measurement of a potential difference in a solution between the two end points of a vibrating probe. The measurement of this ohmic drop can be related to the ionic current flowing between a particular point on a sample and a counter electrode, which is placed far away from the sample, or on the sample itself in the case of local galvanic current measurements. This is determined by Ohm's law and the resistance of the electrolyte layer defined by the movement of the probe.
This Demonstration illustrates the factors influencing the signal measured at the probe. It is based on the assumption that the electrolyte is a homogeneous conductor, with no charge or concentration gradients.
We can derive the value of the potential difference measured by a potentiometric probe located at a height  over the electrode and abscissa
over the electrode and abscissa  , considering a radial symmetry around the axis
, considering a radial symmetry around the axis  , expressed as a function of the potential
, expressed as a function of the potential  applied to the disk electrode and its diameter
applied to the disk electrode and its diameter  :
:

Reference
[1] J. Newman, "Resistance for Flow of Current to a Disk," Journal of the Electrochemical Society, 113(5), 1966 pp. 501–502.
Permanent Citation