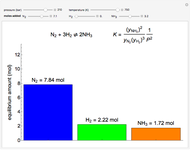
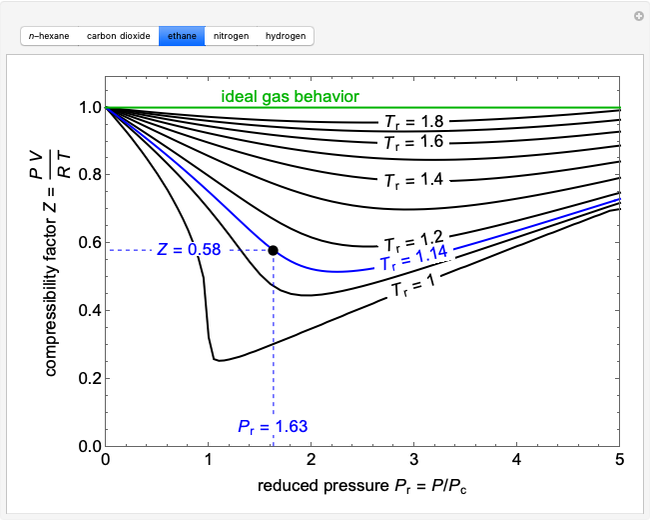
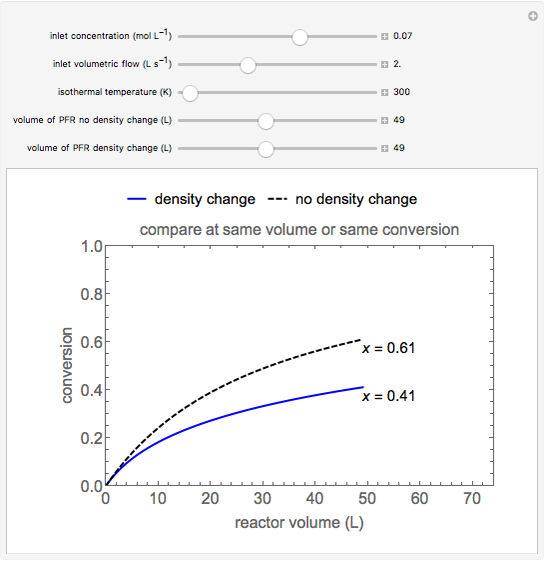
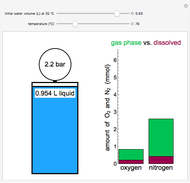
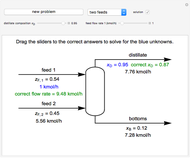
Pressure-Temperature Diagram for a Binary Mixture

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
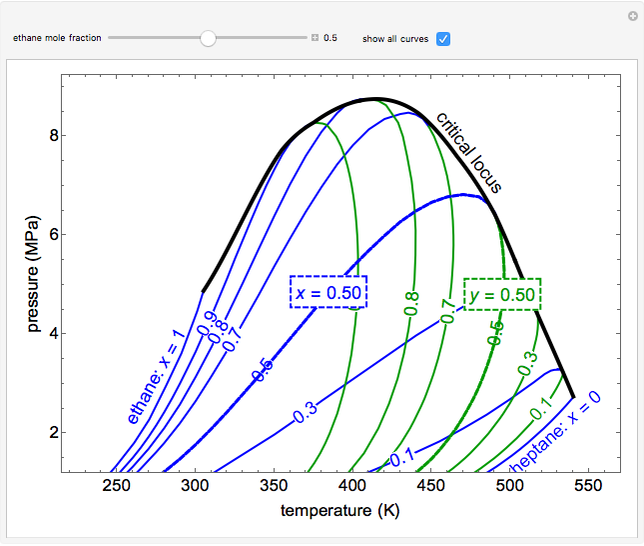
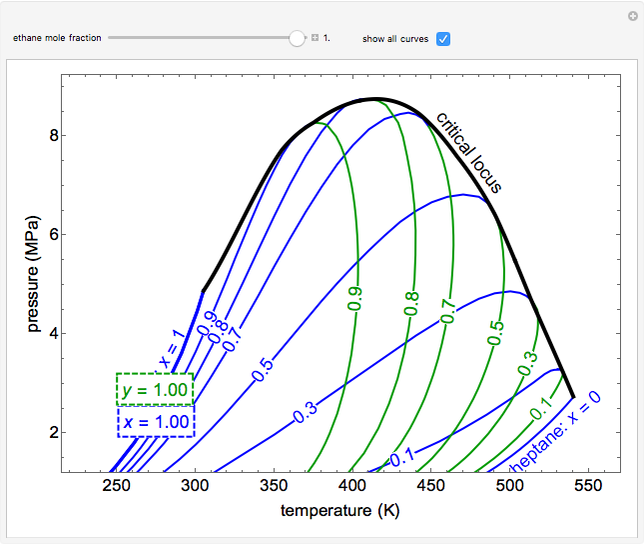
This Demonstration shows a pressure-temperature ( -
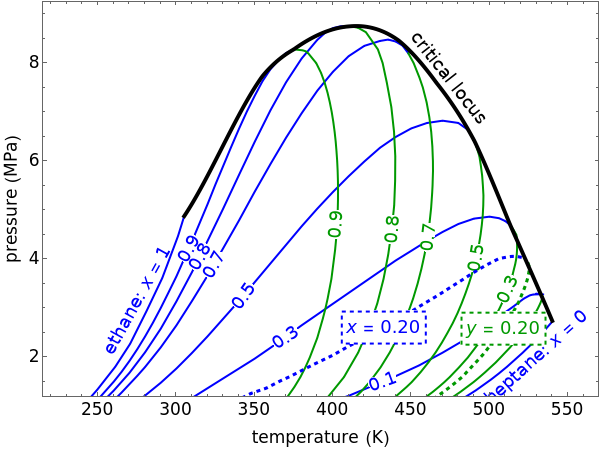
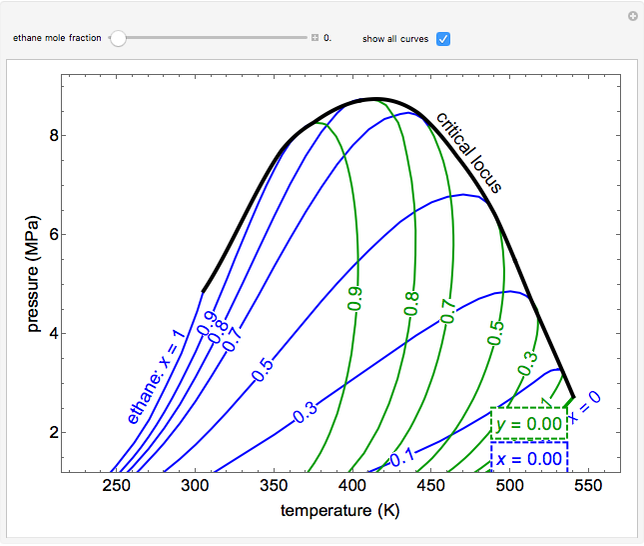
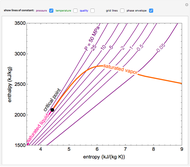
-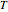 ) diagram for an ethane/heptane mixture in vapor-liquid equilibrium. The single-component plots of saturation pressure as a function of temperature are shown, as are
) diagram for an ethane/heptane mixture in vapor-liquid equilibrium. The single-component plots of saturation pressure as a function of temperature are shown, as are  -
-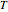 curves at six different ethane mole fractions; the liquid curve is shown in blue, the vapor curve in green. Use the slider to display an additional
curves at six different ethane mole fractions; the liquid curve is shown in blue, the vapor curve in green. Use the slider to display an additional  -
-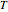 curve (dashed) at the ethane mole fraction selected. The critical locus (black curve) represents the critical points for all mixtures of ethane and heptane. Uncheck "show all curves" to show only the selected mole fraction and the pure components.
curve (dashed) at the ethane mole fraction selected. The critical locus (black curve) represents the critical points for all mixtures of ethane and heptane. Uncheck "show all curves" to show only the selected mole fraction and the pure components.
Contributed by: Adam J. Johnston and Rachael L. Baumann (April 2017)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The bubble-point and dew-point pressures are calculated from Raoult's law:
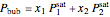 ,
,
 ,
,
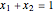 ,
,
The saturation pressures are calculated using the Antoine equations:
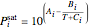 ,
,
where 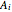 ,
, 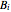 and
and 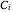 are Antoine constants and
are Antoine constants and 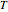 is temperature.
is temperature.
The Peng–Robinson equation of state for mixtures is used to determine the phase envelope and the critical locus. The critical point is where the bubble and dew curves meet; connecting these points is the critical locus. The 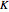 -values are calculated:
-values are calculated:
 ,
,
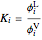 .
.
The fugacity coefficient 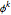 is calculated:
is calculated:
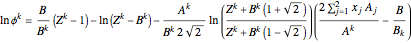 ,
,
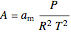 ,
,
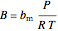 ,
,
where 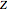 is the compressibility factor, the superscript
is the compressibility factor, the superscript  is for liquid and vapor,
is for liquid and vapor, 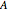 and
and 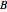 are constants, and
are constants, and  is pressure.
is pressure.
For a mixture:
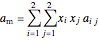 ,
,
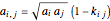 ,
,
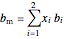 ,
,
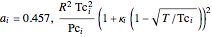 ,
,
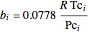 ,
,
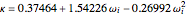 ,
,
where 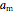 and
and 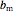 are the attraction and repulsion factors for the mixture,
are the attraction and repulsion factors for the mixture, 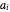 and
and  are the attraction and repulsion parameters for the pure component,
are the attraction and repulsion parameters for the pure component,  is the binary interaction parameter,
is the binary interaction parameter, 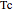 and
and 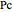 are the critical temperature and pressure,
are the critical temperature and pressure,  is a simplification term, and
is a simplification term, and  is the acentric factor.
is the acentric factor.
The equation 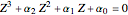 is solved for the compressibility factor,
is solved for the compressibility factor,
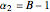 ,
,
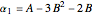 ,
,
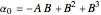 ,
,
where 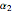 ,
, 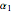 and
and 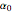 are constants.
are constants.
Reference
[1] J. R. Elliott and C. T. Lira, Introductory Chemical Engineering Thermodynamics, 2nd ed., Upper Saddle River, NJ: Prentice Hall, 2012 pp. 626–628.
Permanent Citation