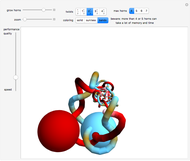
Projections of the 16-Cell

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
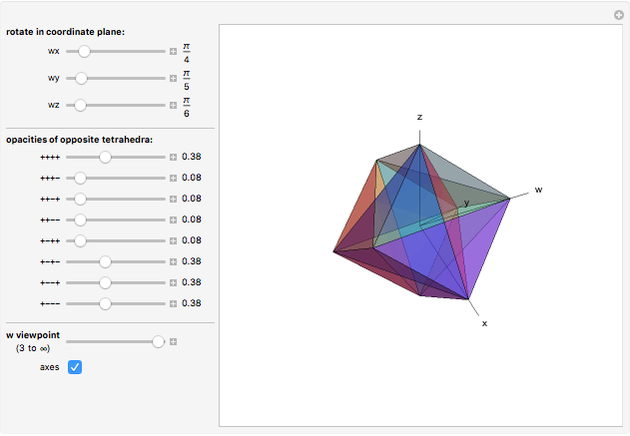
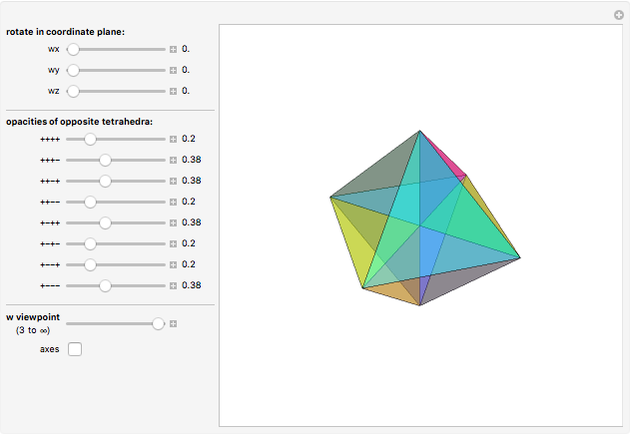
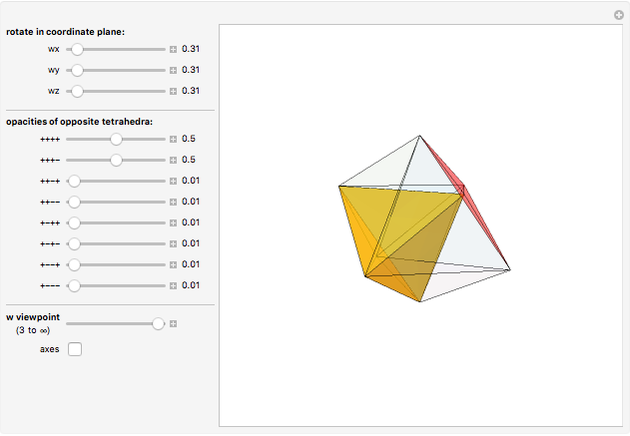
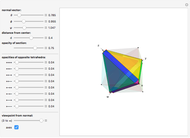
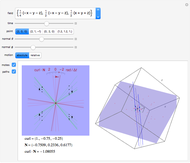
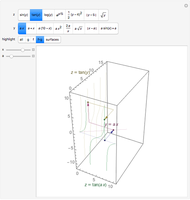
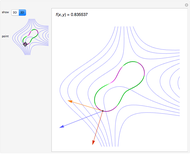
Rotate a four-dimensional regular cross polytope (or 16-cell, Schlaefli symbol {3,3,4}) and project it into three-dimensional graphics. The rotation is the composite of rotations in the  ,
,  , and
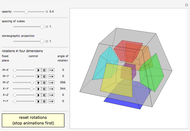
, and  planes, in that order. Opposite tetrahedra (3-cells) of the cross polytope are colored with similar colors. Play with the opacity to see how the cross polytope is bounded by 16 tetrahedra.
planes, in that order. Opposite tetrahedra (3-cells) of the cross polytope are colored with similar colors. Play with the opacity to see how the cross polytope is bounded by 16 tetrahedra.
Contributed by: Michael Rogers (Oxford College/Emory University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A cross polytope is a higher-dimensional analog of the octahedron. The rotation of the 4D cross polytope, whose vertices have coordinates all zero except one either ±1, is the composite of rotations in the  ,
,  , and
, and  planes, in that order. Combined with Mathematica's built-in rotation of 3D graphics, this gives all six degrees of freedom of four-dimensional rotations. The bounding tetrahedra are drawn in the order from least
planes, in that order. Combined with Mathematica's built-in rotation of 3D graphics, this gives all six degrees of freedom of four-dimensional rotations. The bounding tetrahedra are drawn in the order from least  coordinate to greatest. If all the opacities are set to one, the display shows the tetrahedra "visible" from out on the positive
coordinate to greatest. If all the opacities are set to one, the display shows the tetrahedra "visible" from out on the positive  axis. The projection is from a point on the positive
axis. The projection is from a point on the positive  axis onto the
axis onto the  hyperplane; the resulting 3D figure is then projected onto the screen by the normal Mathematica 3D graphics. The positive
hyperplane; the resulting 3D figure is then projected onto the screen by the normal Mathematica 3D graphics. The positive  ,
,  ,
,  , and
, and  axes of the cross polytope may be shown; these rotate with the cross polytope, which helps illustrate how the rotations work. The opacity sliders are labeled according to the nonzero coordinates of the vertices of one of the corresponding pairs of bounding tetrahedra (in the order
axes of the cross polytope may be shown; these rotate with the cross polytope, which helps illustrate how the rotations work. The opacity sliders are labeled according to the nonzero coordinates of the vertices of one of the corresponding pairs of bounding tetrahedra (in the order  ). Each tetrahedron has one vertex on each of the four axes.
). Each tetrahedron has one vertex on each of the four axes.
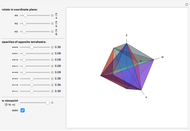
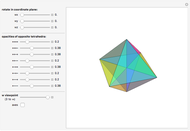
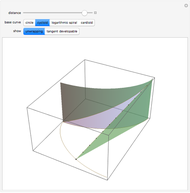
Snapshot 1: projection as a cube (just as the octahedron may be projected as a square)
Snapshot 2: projection as an octahedron
Snapshot 3: projection as a triangular antiprism
Permanent Citation