Proposition 1, Book X, Euclid's Elements

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
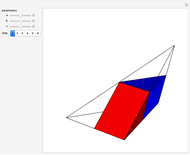
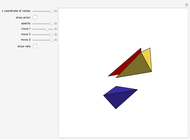
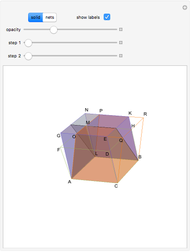
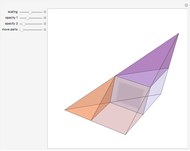
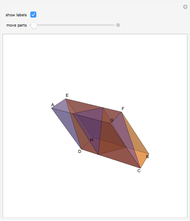
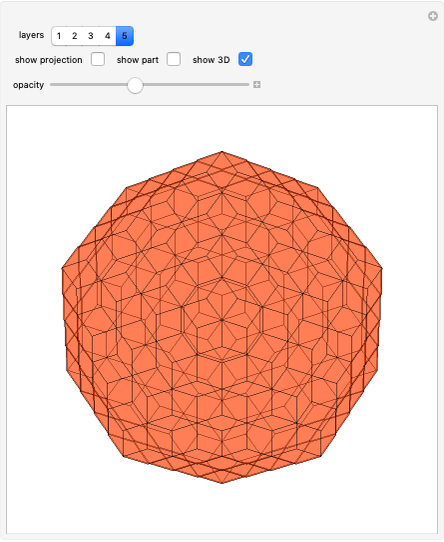
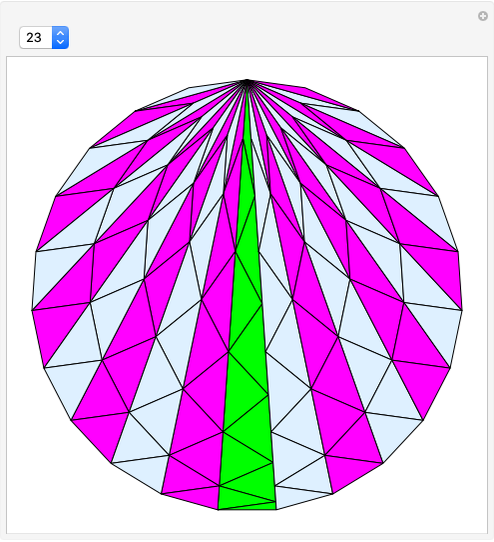
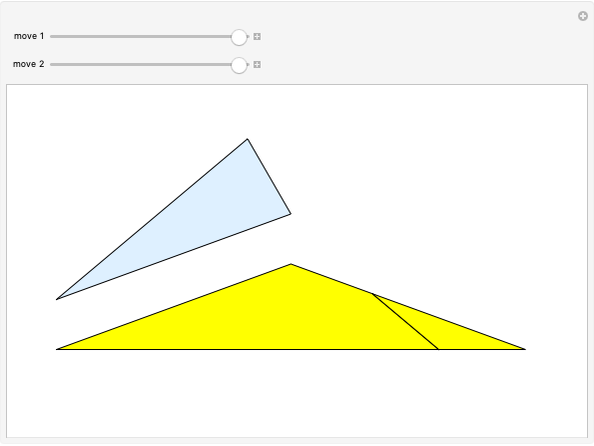
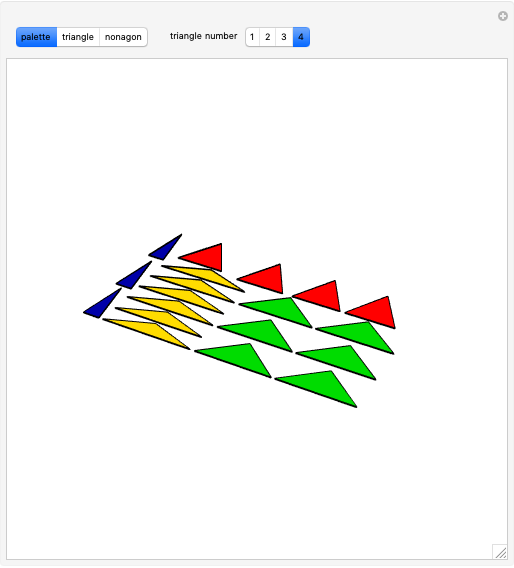
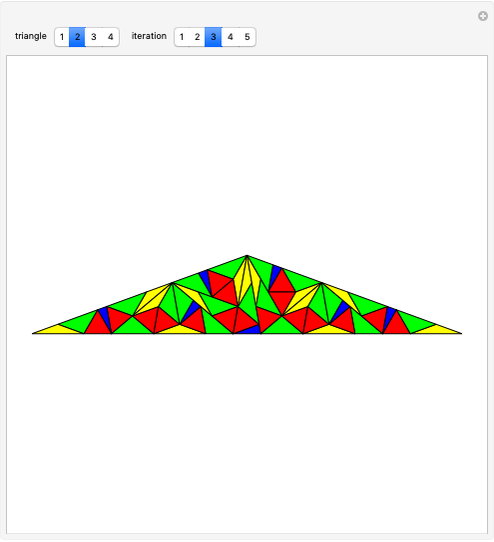
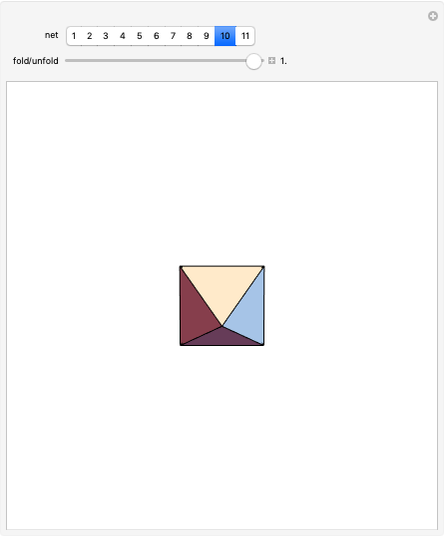
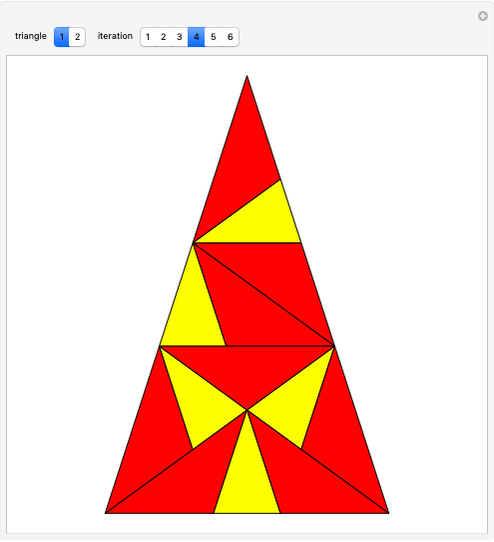
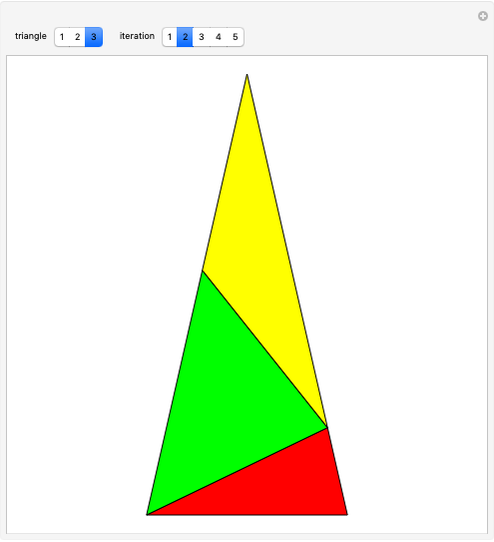
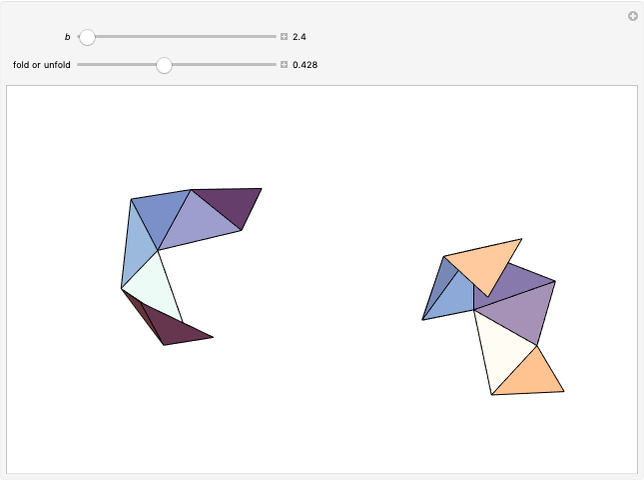
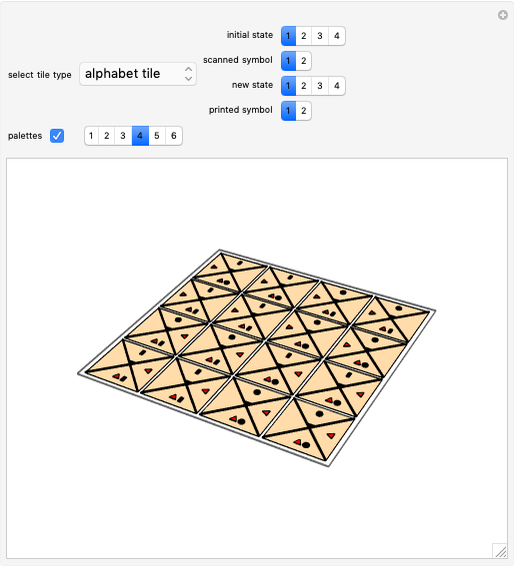
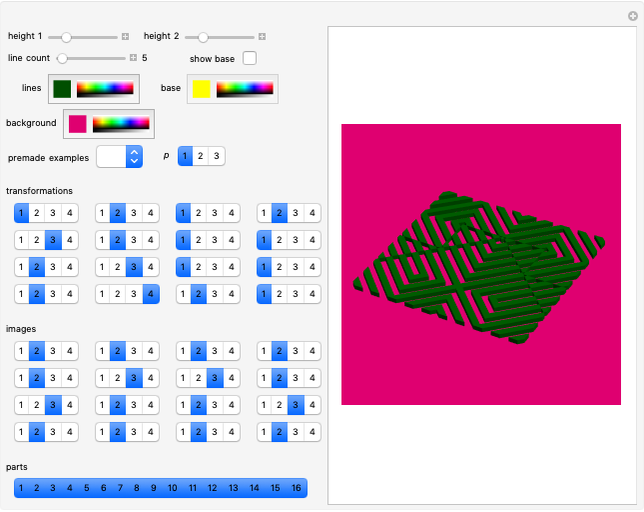
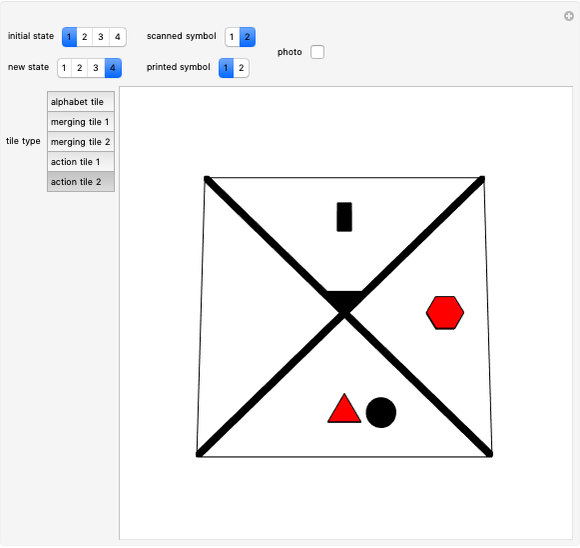
Let  be a positive volume. A triangular pyramid of volume
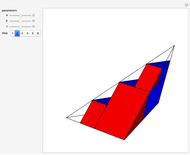
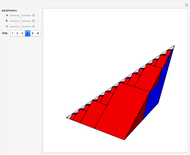
be a positive volume. A triangular pyramid of volume 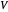 is divided into two similar triangular pyramids and two prisms of equal volume. Each of the two smaller pyramids is divided in the same way, producing four pyramids and four prisms. Eventually at step
is divided into two similar triangular pyramids and two prisms of equal volume. Each of the two smaller pyramids is divided in the same way, producing four pyramids and four prisms. Eventually at step  , the volume of the
, the volume of the 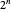 small pyramids will be smaller than
small pyramids will be smaller than 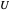 .
.
Contributed by: Izidor Hafner (September 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Proposition 1, Book X
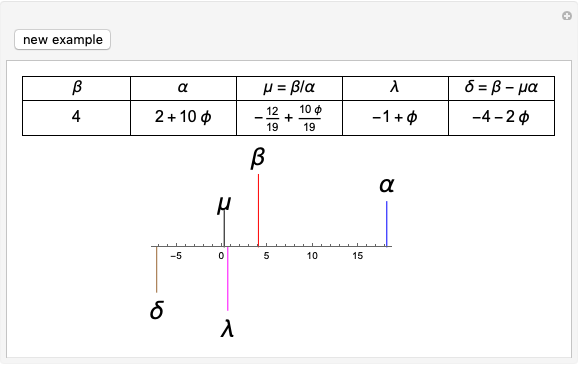
Two unequal magnitudes being set out, if from the greater there be subtracted a magnitude greater than its half, and from that which is left a magnitude greater than its half, and if this process be repeated continually, there will be left some magnitude which will be less than the lesser magnitude set out. [1, p. 14].
Proposition 3, Book XII
Any pyramid which has a triangular base is divided into two pyramids equal and similar to one another, similar to the whole and having triangular bases, and into two equal prisms; and the two prisms are greater than the half of the whole pyramid. [1, p. 378–381].
Proposition 1, Book X is a form of the "axiom of continuity" equivalent to Archimedes's axiom [2, p. 42]. Proposition 1, Book X and Proposition 3, Book XII are then used to prove Proposition 5, Book XII by Eudoxus's method of exhaustion:
Proposition 5, Book XII
Pyramids which are of the same height and which have triangular bases are to one another as the bases. [1, p. 386].
Two triangular-based pyramids of equal height have their volumes in the same ratio as the areas of their bases. [2, p. 43].
References
[1] Euclid, The Thirteen Books of the Elements, Vol. 3, 2nd ed. (T. L. Heath, trans.), New York: Dover Publications, 1956.
[2] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1997.
Permanent Citation